Przy okazji pisania jakiegoś dokumentu o charakterze naukowym w LaTeX-u zdarza mi się liczyć różne rzeczy za pomocą Mathematici. Gdy wynik obliczenia jest prosty można go szybko i bezboleśnie przepisać do LaTeX-a. Czasem niestety okazuje się on być sporym krzakiem. Co wtedy zrobić?

Weźmy dla przykładu takie oto obliczenie, którego wynikiem jest spory pierwiastek:

W menu podręcznym znajuje się opcja “Copy As LaTeX”:

ale wynik jej działania jest tragiczny (a zazwyczaj nie działa). Dla tego przykładu Mathematica skopiowała mi do schowka take oto coś:

\$Failed

Nie jest to zachwycający wynik, więc postanowiłem podejść do problemu inaczej. Znalazłem opis funkcji TeXForm, którą stosuje się w następujący sposób (oczywiście dalej na tym samym przykładzie):

lub tak:

W obydwu powyższych przypadkach Mathematica wypisuje na ekran poprawny (no dobra, z jednym małym błędem) kod LaTeX, który po wpisaniu do dokumentu i kompilacji daje następujący efekt:

Po poprawieniu wspomnianego wcześniej i widocznego powyżej błędu dostajemy:

Fajne, prawda?

goto

Ponieważ w komentarzu do mojego posta o zadaniach dla humanistów pojawiła się kwestia obliczeń numerycznych w programie Mathematica, napiszę o tym teraz.

Gdy próbujemy policzyć w Mathematice prostą rzecz typu:

In: 4*Sqrt[17] + Sin[Pi/5]

Otrzymamy nieciekawe wyrażenie:

Out: 4 Sqrt[17] + Sqrt[5/8 – Sqrt[5]/8]

Zapisując w sensowny sposób nasz wynik wygląda tak:

Ale ile to jest? Użycie opcji Simplify lub FullSimplify nie daje efektu, tego wyrażenia nie da się (zdaniem Mathematici) bardziej uprościć.

Aby otrzymać wynik musimy poprosić Mathematicę o wynik numeryczny poprzez zastosowanie opcji N

Gdy tak zrobimy otrzymamy wynik:

In: 4*Sqrt[17] + Sin[Pi/5] // N
Out: 17.0802

Otrzymaliśmy wynik numeryczny. Może się jednak zdarzyć, że dokładność wyniku nie jest dla nas zadowalająca. Należy wtedy skorzystać z N w trochę innej postaci:

In: N[4*Sqrt[17] + Sin[Pi/5],50]
Out: 17.080207754763115328454345378535380869186449339138

Gdzie drugim argumentem N[] jest liczba cyfr znaczących w wyniku.

goto

Każdy fizyk wie, że świat dookoła najłatwiej opisać równaniem różniczkowym. Reszta (“czyli większość pozostająca w opozycji”) zapewne nie wie, że wzory (np. na ruch wahadełka czy słynnej masy na sprężynce) wypisywane na ściągach w liceum i wcześniej są rozwiązaniami równań różniczkowych opisujących dany problem.

Z powyższego powodu (gloryfikacja równań różniczkowych) chciałbym napisać parę prostych przykładów rozwiązywania równań różniczkowych za pomocą programu Mathematica.

Ponownie sięgnę po zadanie z kolokwium z I roku. Mamy do rozwiązania równanie różniczkowe:

Niezbyt skomplikowane równanie pierwszego rzędu… dałoby się policzyć nawet w pamięci, ale po co?

Prosimy Mathematicę o rozwiązanie:

In: DSolve[x^2 y'[x] == (y[x])^2 + x y[x], y[x], x]
Out: y[x] -> x/(C[1] – Log[x])

Trochę wyjaśnienia o funkcji DSolve. Przyjmuje ona 3 argumenty: równanie (lub równania, o czym zaraz), funkcję jakiej rozwiązania szukamy oraz zmienną niezależną. W naszym przypadku interesuje nas rozwiązanie postaci funkcji y(x), gdzie x jest zmienną niezależną. Przy zapisywaniu równań należy pamiętać że y jest funkcją x (nie piszemy y” tylko y”[x]).

Mathematica zwróciła nam rozwiązanie ogólne:

W zadaniu poproszono nas jeszcze o rozwiązanie tego równania różniczkowego z uwzględnieniem warunku początkowego:

Możemy to zrobić na 2 sposoby:

• Podstawić x=1 do rozwiązania ogólnego i rozwiązać równanie na stałą C1

In: Solve[1/(C1-Log[1])==1,C1]
Out: C1 -> 1

• Uwzględnić warunek początkowy przy rozwiązywaniu równania poprzez DSolve (jako pierwszy argument podajemy dwa równania ujmując je w klamry {} i oddzielając przecinkiem):

In: DSolve[{x^2 y'[x] == (y[x])^2 + x y[x],y[1]==1}, y[x], x] //Simplify
Out: y[x]->x/(1-Log[x])

Jak widać obydwie metody prowadzą nas do tego samego wyniku:

Przy bardziej skomplikowanych równaniach mających więcej warunków początkowych druga metoda okazuję się być zdecydowanie bardziej efektywna.

Ostatnią rzeczą o którą prosił nas autor jest narysowanie otrzymanego rozwiązania:

In: Plot[x/(1 – Log[x]), {x, 0, 6}, {Exclusions -> {1 – Log[x] == 0},
ExclusionsStyle -> Dashing[Small], PlotRange -> 50}]

Otrzymujemy:

Tak więc wiemy już jak zabrać się za rozwiązywanie nieskomplikowanych równań różniczkowych. Następnym razem pobawimy sie macierzami

goto

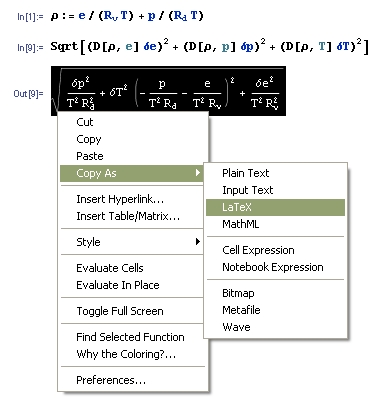
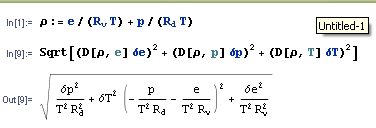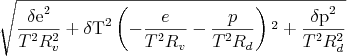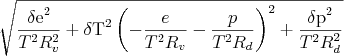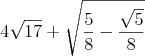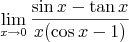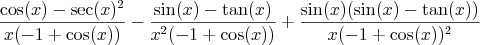Znalazłem dzisiaj za biurkiem zeszłoroczny egzamin z analizy I C. Postanowiłem się pobawić Mathematicą i porozwiązywać zadania nie wysilając własnej szarej komórki.

Ponieważ to część pierwsza przykłady będą banalne, ale dające ładne efekty 🙂

Poniżej podzielę sie wnioskami z rozwiązywania drugiego przykładu z piątego zadania za pomocą programu Mathematica. Zadanie da się rozwiązać od razu więc nadprogramowo się nim pobawimy (a co za tym idzie pobawimy się Mathematicą, a na tym najbardziej nam zależy).

Zadanie: należy obliczyć następującą granicę:

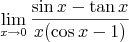
Nic prostszego! Na początek zdefiniujmy sobie funkcję, której granice będziemy liczyć:

In:= k[x_] = (Sin[x] – Tan[x])/(x (Cos[x] – 1))

Teraz możemy przeprowadzać różne operacje na tej funkcji. Policzmy granicę, o którą pytają nas w zadaniu:

In:= Limit[k[x], x -> 0]
Out:= 1

Jak widać granica tej funkcji przy x dążącym do zera wynosi 1.

Niby rozwiązaliśmy zadanie, ale mnie nadal ciekawi jak ta funkcja wygląda (te trygonometryczne zawsze są ładne). Narysujmy więc:

In:= Plot[k[x],{x,-2*Pi,2*Pi}]

Jako wynik otrzymujemy wykres:

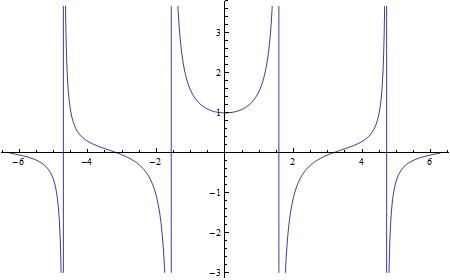
Funkcja ładna, rzeczywiście dąży do 1 dla x dążącego do 0, ale wykres jeszcze nie bardzo. Poprawmy te pionowe krechy (poprzez wyłączenie punktów krytycznych z wykresu):

In:= Plot[k[x],{x,-2*Pi,2*Pi}, {Exclusions -> {Tan[x] == 0}}]

Otrzymujemy:

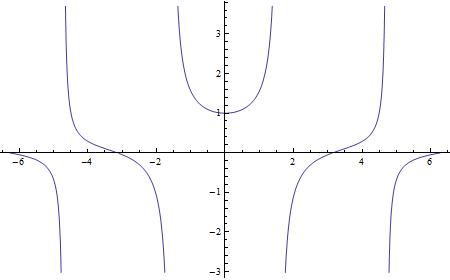
Już ładniej, ale zrobiło sie trochę “łyso”. Przydałyby się asymptoty:

In:= Plot[k[x],{x,-2*Pi,2*Pi}, {Exclusions -> {Tan[x] == 0}, ExclusionsStyle -> Dashing[Small]}]

Otrzymujemy:

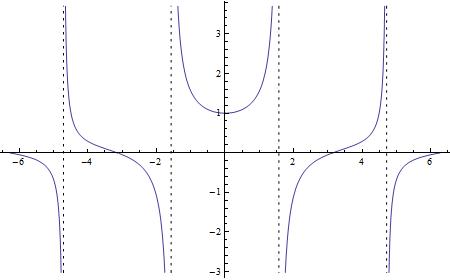
Teraz otrzymaliśmy (przez zastosowanie dwóch opcji) bardzo ładny wykres funkcji z zadania.

Funkcje mające ładne wykresy mają zazwyczaj ładne pochodne. Ta nie jest wyjątkiem. Obliczamy pochodną funkcji po x:

In:= D[k[x],x]

Mathematica zwraca nam przepiękny wzór na pochodną naszej funkcji:

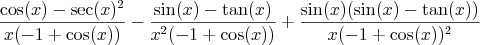
Który po uproszczeniu (polecenie Simplify[]) przyjmuje następującą postać:

sec to secans, czyli stosunek przeciwprostokątnej i przyprostokątnej przyległej do kąta ostrego a więc odwrotność cosinusa.

Narysujmy sobie jeszcze tą pochodną:

In:= Plot[{(x Sec[x]^2 – Tan[x])/x^2}, {x, -2*Pi, 2*Pi}]

Otrzymany wykres wygląda następująco:

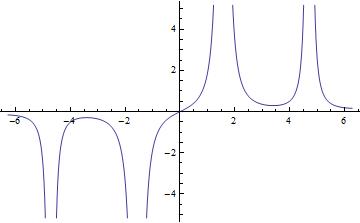
Ładny, prawda?

goto