Przez ostatnie 4 lata prowadziłem na Wydziale Fizyki ćwiczenie do kilku kursów programowania w pythonie i c++. Kilka razy spotkałem się z pytaniem o liczby zmiennoprzecinkowe. Poruszamy na zajęciach kwestię zapisu binarnego liczb całkowitych i wtedy pojawia się pytanie o liczby rzeczywiste. Do tej pory odpowiadałem bardzo skrótowo, że “jest to skomplakowne”, bardzo sprytne, ale nie pozbawione wad. W przypadku liczb całkowitych sprawa jest prosta. W danej ilości bitów możemy przechować dany zakres liczb całkowitych. Z liczbami zmiennoprzecinkowymi problem polega na tym, że w każdym przedziale jest ich nieskończenie wiele, a my mamy tylko 32 albo 64 bity. Więc jak to właściwie jest? O samej formie zapisu można oczywiście przeczytać wszystko w Wikipedii – ja chcę zrobić eksperyment. Na pierwszy ogień liczby typu float, czyli 32 bitowe (1 bit na znak, 8 bitów na wykładnik i 23 na mantysę). 32 bity daje jakieś 4 294 967 296 kombinacji – to na tyle mało, że mogę sprawdzić wszystkie. W ramach testu sprawdzam ile liczb mieści się w 4 przedziałach: 0-1, 1-2, 1000-1001 i 1000000-1000001:

int main()
{
	float f;
	uint i;	 
	std::vector range = {0, 1, 1000, 1000000};
	std::vector count = {0, 0, 0, 0};
	for(i = 0; i=range[a] && f < range[a]+1)
				count[a]++;
		}
	}
	for(int a = 0; a < range.size(); a++)
	{
		std::cout << range[a] << "-" << range[a]+1 << ":\t" << count[a] << std::endl;
	}
}

Wynik mamy po niecałych 2 minutach. Policzone ilości liczb są bardzo ciekawe:

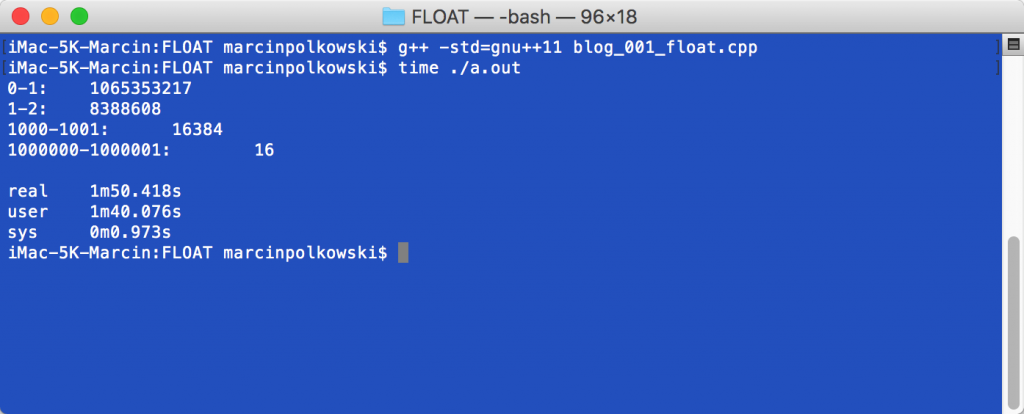
Od razu widać kilka zależności. W zakresie od 1 do 2 jest dokładnie 2^23 liczb - tak jakby były to wszystkie "mantysy" dla jednego wykładnika. W zakresie od 0 do 1 jest dokładnie 2^23*(2^7-1)-1 - czyli wszystkie mantysy dla połowy wykładników (bez jednego). Im większa liczba tym mniejsza dokładność - mamy do dyspozycji 2^31 a musimy móc pokazać zarówno bardzo małe liczby i te gigantyczne.

Z liczbami w pojedynczej precyzji sprawa była prosta - udało się sprawdzić wszystkie kombinacje w niecałe 2 minuty. Przy podwójnej precyzji mamy 64 bity, więc sprawdzenie wszystkich zajęłoby 16000 lat. Szkoda czasu. Możemy natomiast pobawić się takim kodem:

int main()
{
	union
	{
		uint64_t input;
		uint64_t   output;
	} data;

	uint64_t x = 5;
	data.input = x;
	std::bitset   bits(data.output);

	for(uint64_t a = 0; a<=2048; a++)
	{
		for(uint64_t b = 0; b<=pow(2,52)-1; b+=pow(2,52)-1)
		{
			x = b+(a<<52);
			data.input = x;
			bits = data.output;
			double f;
			memcpy(&f, &x, sizeof(f));
			std::cout << std::setw(4)<< a<< '\t'<< std::setw(16)<<  b << '\t'<< std::setw(12) << f << '\t' << bits  << std::endl;
		}
		std::cout << std::endl;
	}
}

Powyższy kod wypisze zakres liczb dla każdego z 2^11 wykładników. Mantysa ma 52 bity (~4.5*10^15), więc od 1 do 2 mamy właśnie 2^52 liczb, Tyle samo od 2 do 4, 4 do 8 itd:

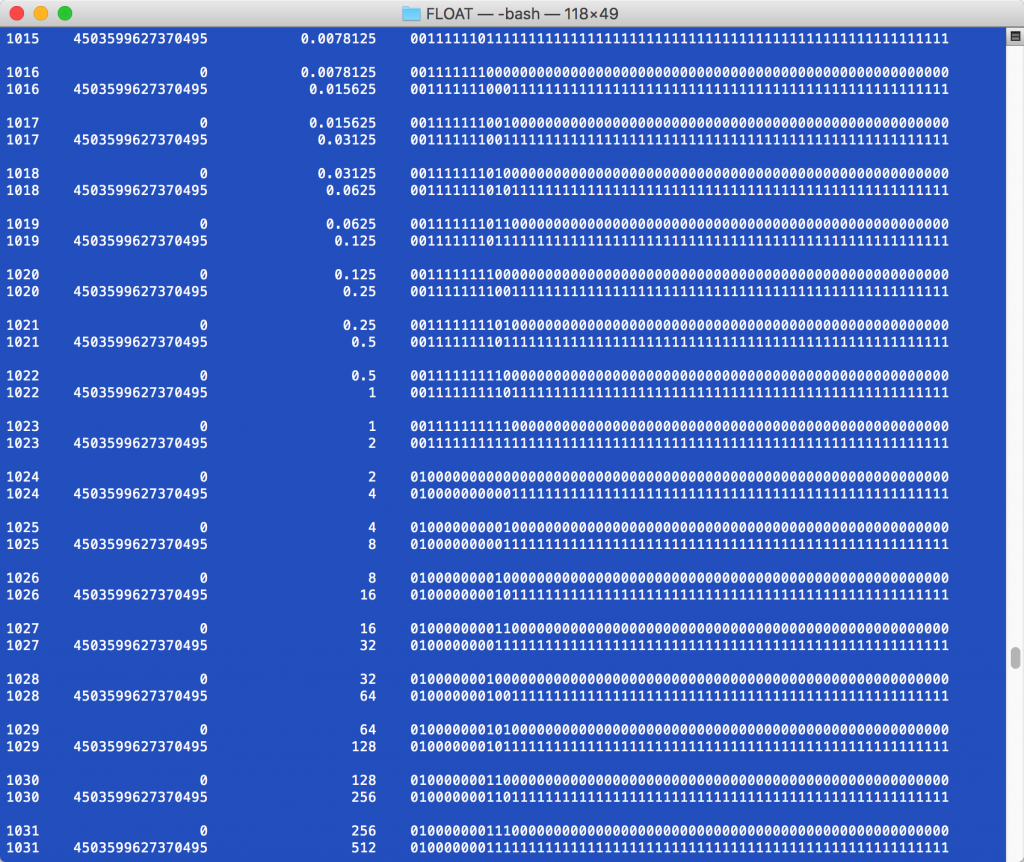
Na powyższym przykładzie pierwsza kolumna to wykładnik, druga to mantysa, trzecia to wartość liczby, a czwarta to reprezentacja binarna.

Nie chcę tutaj wnikać w szczegóły samego formatu. Zależy mi na pokazaniu specyfiki takiego pamiętania liczb. Możecie modyfikować i uruchamiać powyższe kody, a dowiecie się więcej o liczbach zmiennoprzecinkowych. Dodatkowo powyższe przykłady powinny dobrze obrazować kolosalną różnicę pomiędzy pojedynczą i podwójną precyzją.

Musimy pamiętać, że operując na bardzo dużych liczbach, gdzie dokładność zapisu zmiennoprzecinkowego jest mała, możemy wprowadzać błędy numeryczne - w szczególności gdy łączymy wielkie i małe liczby.

Kto dowiedział się czegoś nowego klika łapkę w górę!