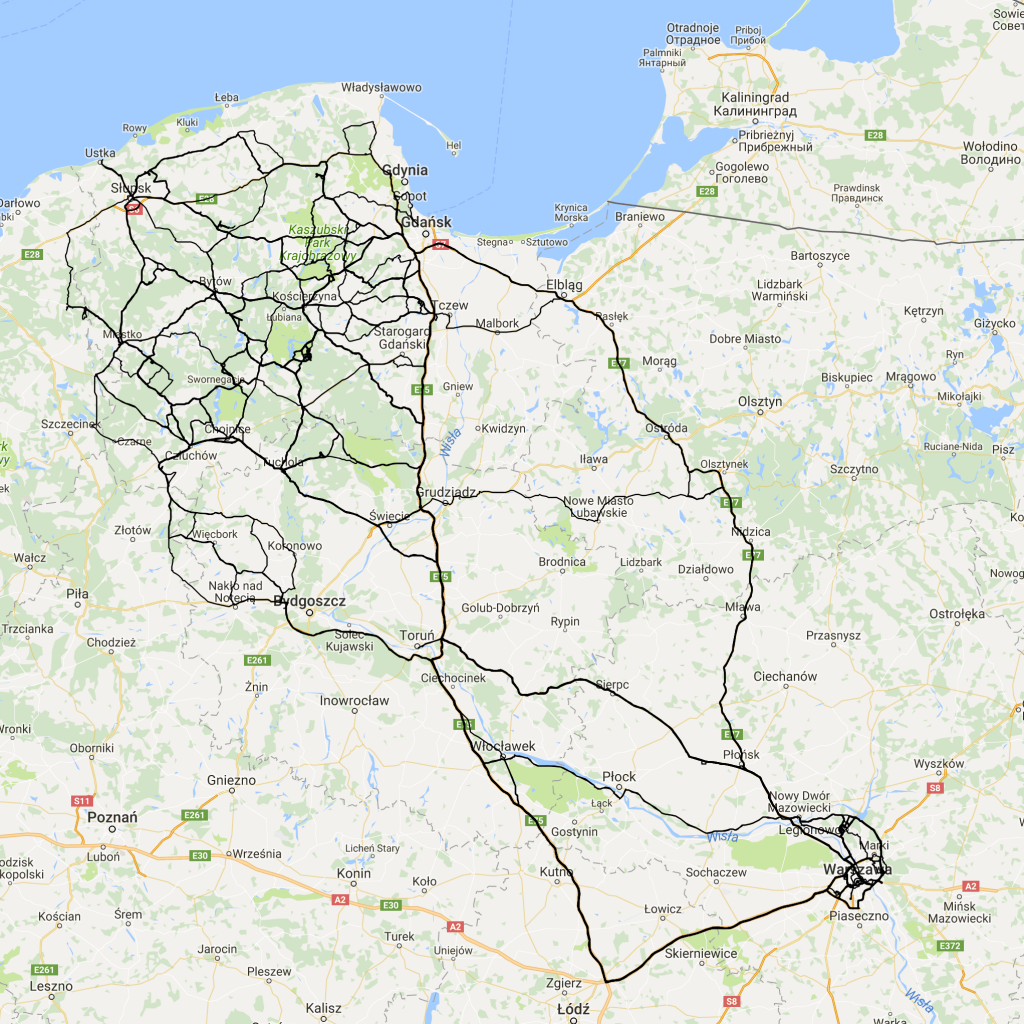
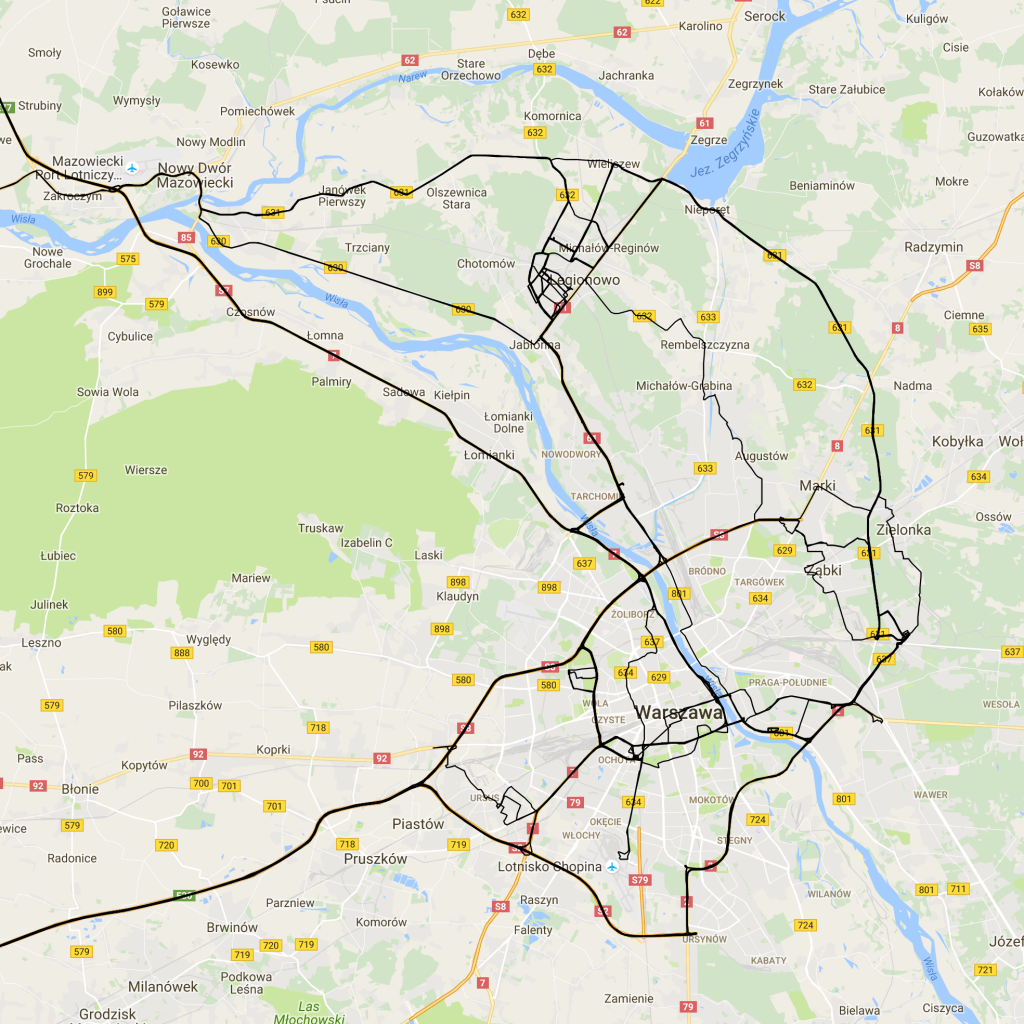
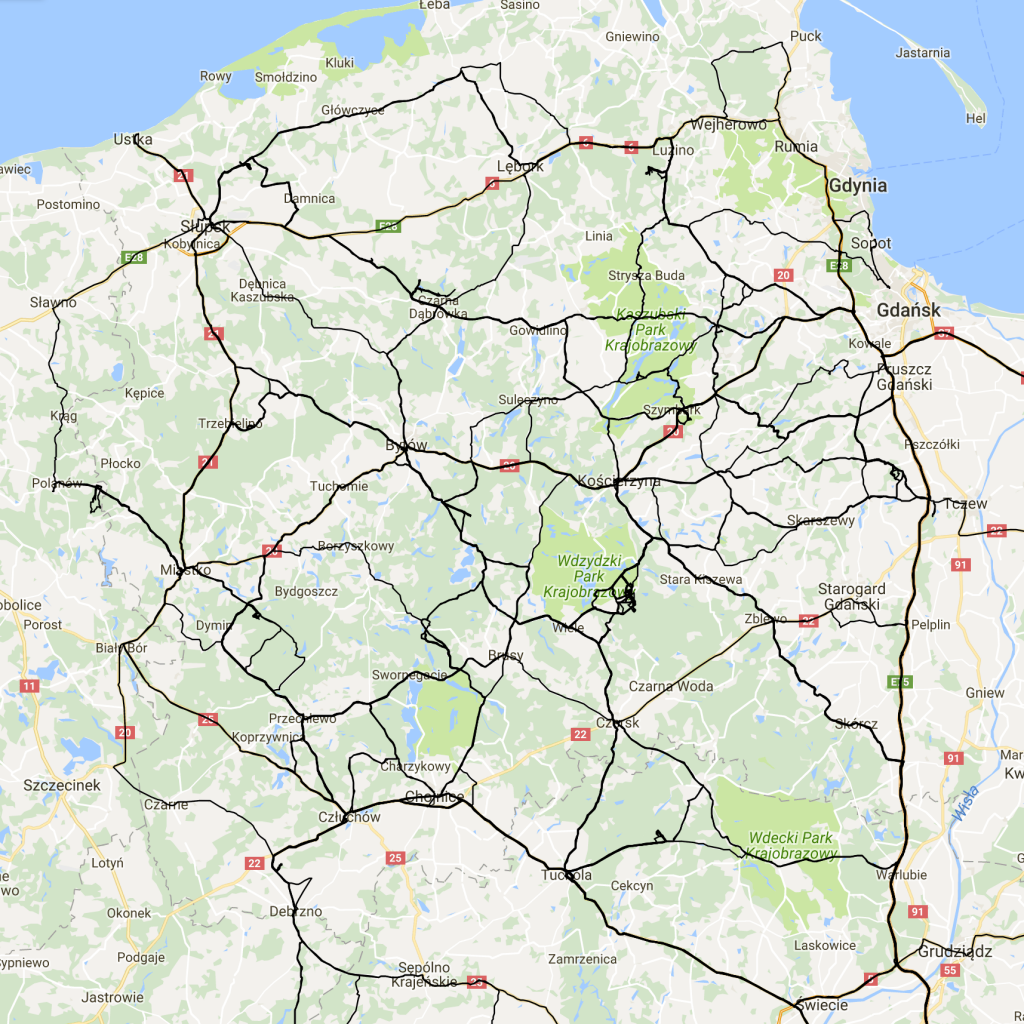
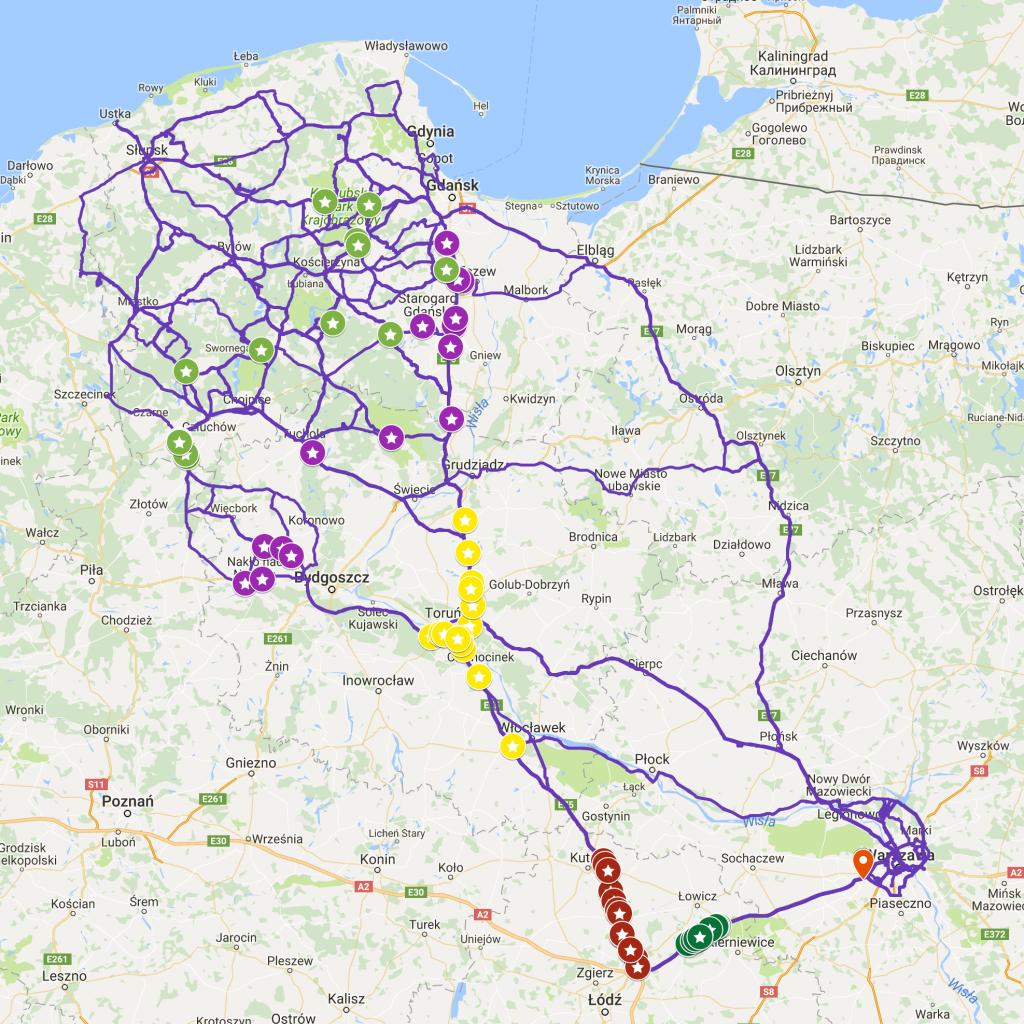
Od czterech lat biorę udział w pasywnym eksperymencie sejsmicznym “13BB star”. Będę na ten temat pisał jeszcze wiele razy, ale muszę tutaj zrobić dwa zdania wstępu. Celem eksperymentu jest rejestracja naturalnych zjawisk sejsmicznych, co pozwala na określanie głębokich struktur w Ziemi. W ramach eksperymentu na pomorzu pracowało 13 samodzielnych stacji poukrywanych głęboko w lasach. Każda ze stacji wyposażona była w odbiornik GPS, których celem było dostarczanie bardzo precyzyjnych informacji o czasie. Gdzieś na boku i przy okazji raz na godzinę każda stacja zapisywała pozycję według gps: długość i szerokość geograficzną oraz wysokość n.p.m.
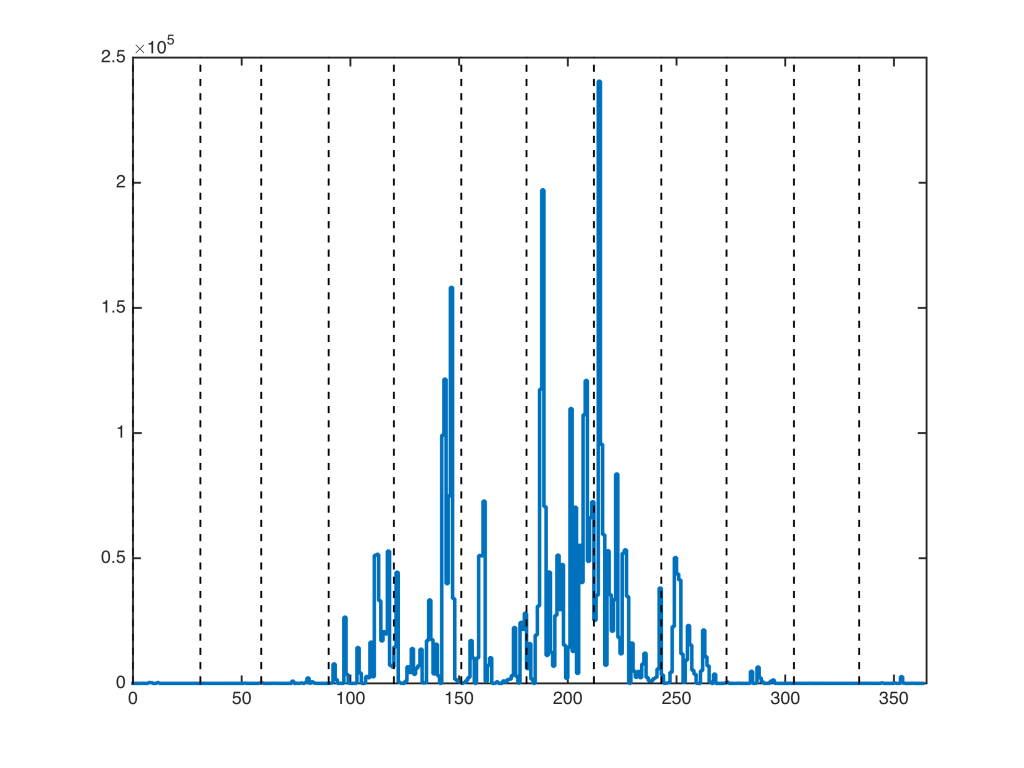
Któregoś dnia postanowiłem wczytać do matlaba te dane dla jednej ze stacji. Gdy narysowałem wykres zależności mierzonej wysokości n.p.m. od czasu zainteresowała mnie mało widoczna zmiana sezonowa. Zupełnie nie dziwi rozrzut pomiarów o +- 10 metrów, bo pomiary “cywilnym” (jako przeciwieństwo do geodezyjnego) GPS są obarczone mniej więcej takim błędem. Zaciekawiło mnie sezonowe przesunięcie pomiarów, które jest bardzo dobrze widoczne po narysowaniu tygodniowej średniej kroczącej:
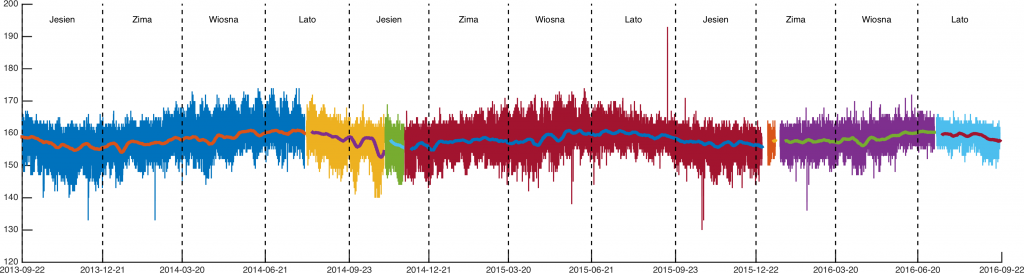
Sprawdziłem od razu czy podobny efekt widać na pozostałych stacjach:
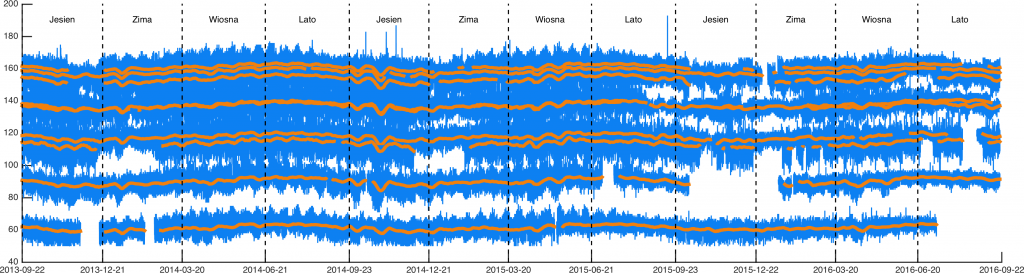
Jeszcze ciekawej sprawa wygląda gdy porówna się średnie kroczące dla wszystkich stacji poprzez odjęcie średniej z całego okresu. Poniżej średnie 7-dniowe:
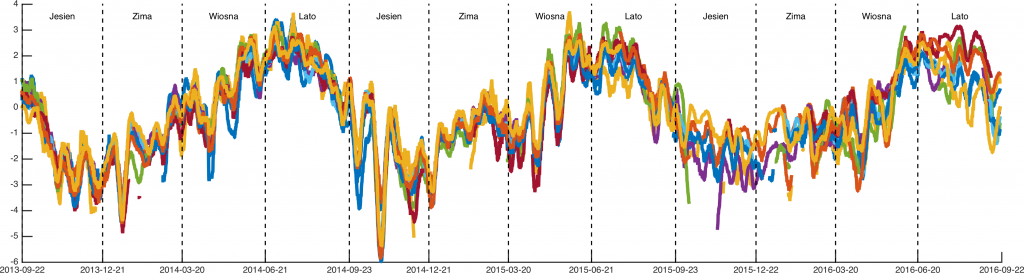
30-dniowe:
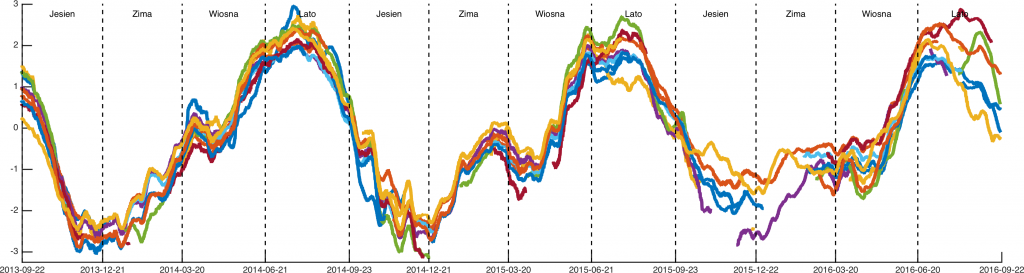
i 60-dniowe:
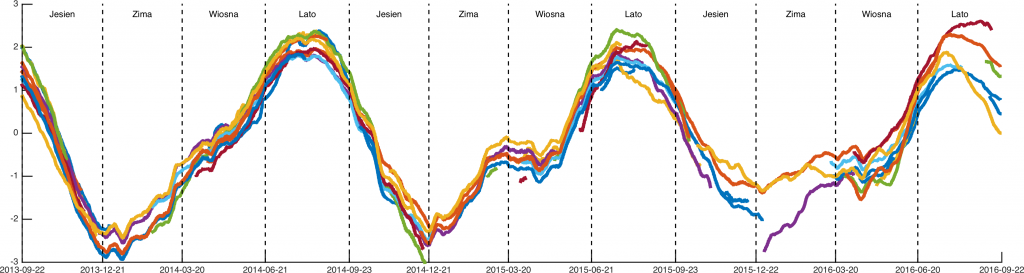
Na powyższych wykresach widać wyraźną sezonowość zmian. Poprosiłem o komentarz specjalistę od pomiarów referencyjnych GPS: “jonosfera, standard, nuda”. Natomiast dla mnie ciekawe jest, że skoro efekt jest tak dobrze znany i tak powtarzalny, czemu nie została wprowadzona na to poprawka. To właśnie dynamika zmian jonosfery powoduje, że cywilne GPS mają ograniczoną dokładność. Sprzęt geodezyjny wykorzystuje stacje permanentne, dzięki którym można określi wpływ jonosfery na pomiar w danym momencie (stacja permanentna się nie rusza, więc odchylenie pomiaru wynika właśnie ze zmian w jonosferze). Takich szybkich lokalnych zmian nie da się przewidzieć, ale zmiany między latem a zimą wydają się całkowicie powtarzalne i oczywiste.
Gdyby ktoś był zainteresowany kodem użytym do wygenerowania 3 dolnych rysunków:
%% 7 dni
clf; hold on
files = dir('*.gps');
colors = lines(length(files));
for fi = 1:length(files)
X = load(files(fi).name);
D = X(:,1) - circshift(X(:,1),[1 0]);
idx = [1; find(D>1); length(X(:,1))]; % Szukanie przerw w danych większych niż 1 dzień
X(X(:,4)>500,4)=NaN;
X(X(:,4)<50,4)=NaN; % Usuwanie pomiarów "od czapy"
for a = 1:length(idx)-1
i = idx(a):idx(a+1)-1;
i(isnan(X(i,4)))=[];
f = nanmean(X(:,4)); % Średnia dla całego okresu
if length(i) > 7*24 % Badamy tylko fragmenty o długości > 7 dni
% Obliczenie i narysowanie średniej kroczącej przesuniętej o średnią globalną
plot(X(i,1), tsmovavg(X(i,4),'s',7*24,1)-f, 'Color', colors(fi,:), 'LineWidth',3)
end
end
end
% Rysowanie i podział rysunku na pory roku
axis([datenum(2013,09,01) datenum(2016,07,31), -6 4])
pory = [datenum(2013,09,22) datenum(2013,12,21) datenum(2014,03,20) datenum(2014,06,21) datenum(2014,09,23) datenum(2014,12,21) datenum(2015,03,20) datenum(2015,06,21) datenum(2015,09,23) datenum(2015,12,22) datenum(2016,03,20) datenum(2016,06,20) datenum(2016,09,22)];
names = {'Wiosna', 'Lato', 'Jesien', 'Zima'};
for a = 1:length(pory)-1
text(mean(pory(a:a+1)),3.5,names{rem(a+1,4)+1},'HorizontalAlignment', 'Center', 'FontSize', 15);
plot([pory(a) pory(a)], [-10 10],'k--')
end
set(gca,'xTick', pory)
datetick('x','YYYY-mm-dd','keepticks')
hgexport(gcf, '13BB_GPS_003_7.png', hgexport('factorystyle'), 'Format', 'png', 'resolution', 300, 'Width', 40, 'Height', 10);