Można by się zastanawiać, po co babrać się w najstarszym języku programowania wysokiego poziomu. Ja jednak im dłużej w nim się babrzę twierdzę, że ma on wiele zalet i osoby zajmujące się dziedzinami naukowymi i inżynierskimi (jak na przykład fizycy) powinny go znać.

Do zalet języka należą:

• Kod jest niezmiernie prosty.
• Posiada typ complex (tryb liczb zespolonych).
• Programy są bardzo szybkie.
• Ogromna liczba bibliotek.
• Przenośność kodu pomiędzy systemami operacyjnymi.

Oczywiście są też wady:

• XXI wiek, a programy fortranowskie działają w “czarnym okienku”.
• Z powodu trybu implikowanego można się pomylić.
• Problematyczne operacje na łańcuchach znaków.

Niedługo na Blogu zaczną pojawiać się artykuły dotyczące nauki programowania w Fortranie, a następnie gdy złożą się one na mały kurs, zacznę opisywać rozwiązania konkretnych problemów.

much.

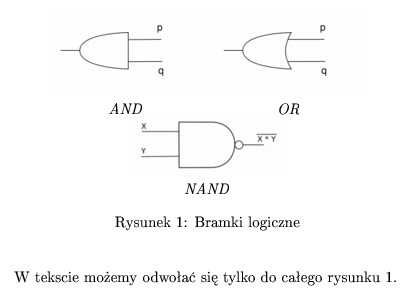
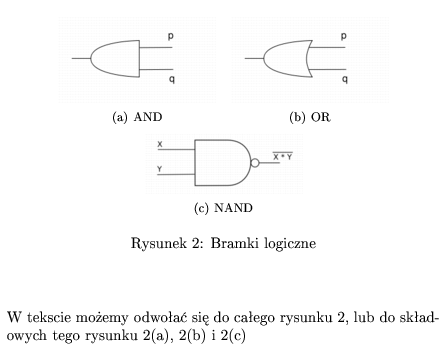
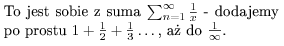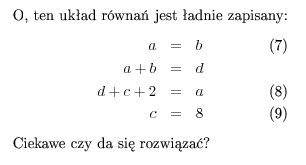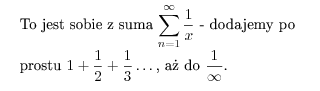Witam, przed nami kolejna część przygód w LeTeX’u (czyt. lateszku). Dzisiaj coś dla początkujących, czyli parę słów o różnych odsłonach trybu matematycznego.

Najprostszym przykładem trybu matematycznego jest umieszczanie symboli matematycznych bądź równań bezpośrednio w treści (w środku zdania) dokumentu:

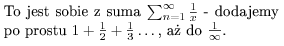
Jak widać w przestawionym poniżej kodzie potrzebnym do wygenerowania powyższego napisu tryb matematyczny wewnątrz tekstu otrzymujemy za pomocą znaków $.

To jest sobie z suma $\sum_{n=1}^{\infty}\frac{1}{x}$
- dodajemy po prostu $1+\frac{1}{2}+\frac{1}{3}\dots$,
aż do $\frac{1}{\infty}$.

Ważne równania wymagają wyróżnienia, którym zazwyczaj jest umieszczenie w nowej linii:

Kod potrzebny do wygenerowania takiego dokumentu przedstawiam poniżej. Zauważ, że powyższe równanie nie zostało ponumerowane. Taki tryb matematyczny uruchamiamy podwójnym znakiem dolara: $$ (i tak samo zamykamy).

Poniższe równanie jest przykładem równania nienumerowanego:
$$a=x+\frac{1}{x}+\frac{1}{x^2}+\dots$$
Widać, że jest ono bardzo ciekawe.

Często równania trzeba numerować, żeby potem móc się do nich odwołać w dokumencie:

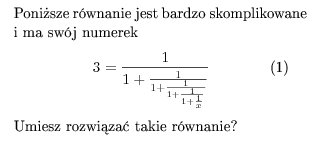
Kod potrzebny do wygenerowania takiego dokumentu przedstawiam poniżej:

Poniższe równanie jest bardzo skomplikowane i ma swój numerek
\begin{equation}
3=\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{x}}}}}
\end{equation}
Umiesz rozwiązać takie równanie?

Jak widać uruchomienie trybu matematycznego z numerowaniem wymaga napisania niekrótkiego kawałka kodu, więc proponuję zdefiniowanie własnego “początku” i “końca” numerowanego trybu matematycznego. Na przykład w taki sposób (kod ten należy umieścić w preambule dokumentu):

\renewcommand{\[}{\begin{equation}}
\renewcommand{\]}{\end{equation}}

Teraz możemy otwierać tryb matematyczny znakami \[ i zamykać \].

Często zdarza się potrzeba zapisania układu równań. Można to zrobić na dwa sposoby:

Jak widać nasz układ równań wygląda bardziej jak cztery zupełnie sobie obce równania. Powyższy układ wygenerowałem następującym kodem:

Poniżej mamy układ równań, który jest bardzo brzydko zapisany:
\[a=b\]
\[a+b=d\]
\[d+c+2=a\]
\[c=8\]
Można by go ładniej zapisać!

Można było to zrobić o wiele ładniej stosując specjalne środowisko matematyczne do układów równań:

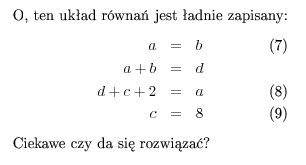
Poniżej kod potrzebny do wygenerowania ładnego układu równań. Zwróć uwagę na celowe wyłączenie numerowania drugiego równania:

O, ten układ równań jest ładnie zapisany:
\begin{eqnarray}
a&=&b\\
a+b&=&d\nonumber\\
d+c+2&=&a\\
c&=&8
\end{eqnarray}
Ciekawe czy da się rozwiązać?

To są właśnie cztery podstawowe typy trybów matematycznych w LaTeX’u. Warto jednak czasami popracować nad wyglądem równań. Poniżej przedstawię modyfikacje dwóch powyższych przypadków za pomocą polecenia \displaystyle:

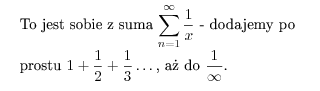
Powyższe zdanie wygenerowałem następującym kodem (porównaj z pierwszym przykładem):

To jest sobie z suma $\displaystyle\sum_{n=1}^{\infty}\frac{1}{x}$
- dodajemy po prostu $\displaystyle1+\frac{1}{2}+\frac{1}{3}\dots$,
aż do $\displaystyle\frac{1}{\infty}$.

Porównaj to równanie z trzecim przykładem. Oto kod:

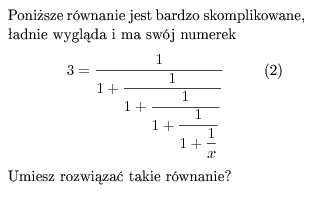
Poniższe równanie jest bardzo skomplikowane, ładnie wygląda i ma swój
numerek\begin{equation}
\frac{1}{\displaystyle 1+\frac{1}{\displaystyle 1+\frac{1}{\displaystyle 1+
\frac{1}{\displaystyle 1+\frac{1}{x}}}}}
\end{equation}
Umiesz rozwiązać takie równanie?

goto

Tak jak obiecałem wczoraj napiszę parę słów o prezencie, który sobie kupiłem pod choinkę, a mianowicie o płaskiej klawiaturze firmy Apple. Jest to model zaprojektowany specjalnie dla nowego modelu iMaca.

Na wstępie chciałbym zaznaczyć, że kiepski ze mnie miłośnik produktów tej firmy, a właściwie można powiedzieć, że omijam jabłuszka szerokim łukiem.

Wszystko zaczęło się jakiś tydzień przed świętami. Byłem sobie w sklepie z szeroko pojętą elektroniką i natrafiłem na stoisko Apple. Mój wzrok przyciągnęła ta właśnie płaska, biała, metalowa klawiatura. Pomyślałem, że to kolejny gadżet Apple’a a coś mnie podkusiło, żeby spróbować jak się na tym pisze. Bosko. Pomyślałem że muszę ją mieć (no i mam). Nie kupiłem od razu (wszystkie dziwne pomysły na wydawanie pieniędzy wymagają okresu wylęgania) lecz po paru dniach. W Polsce klawiatura kosztuje 229 zł, a w USA 49$ – barbarzyństwo! Od razu zapakowałem oryginalne pudełko w papier prezentowy, żeby mnie nie kusiło, bo to przecież pod choinkę.

Prezent rozpakowałem wczoraj. Bardzo skromne, białe pudełko z widokiem boku klawiatury (kliknij, aby powiększyć):

Z boku pudełka znajduje się mała nalepk z informacją “designed by apple in california” oraz “made in china. Najs najs…

W pudełku znajduje się klawiatura, przedłużacz USB, książeczka (pewnie jakieś warunki gwarancji, nie otwierałem).

Klawiatura wygląda bardzo ładnie. Układ klawiszy jest przemyślany, aczkolwiek widać, że nie jest to produkt do PC. Jedyną wadą (w moim przekonaniu) jest pozycja prawego ALT’a, potrzebnego do pisania polskich krzaczków (kliknij, aby powiększyć):

Na klawiaturze pisze się (tak jak pisałem wcześniej) bardzo wygodnie (trzeba tylko przekonfigurować w systemie pozycję tego ALT’a). Po podłączeniu do PC (Win XP) system wykrywa “Apple Keyboard”. Nie ma problemu z kompatybilnością. Niektóre klawisze różnią się od tych w standardowych klawiaturach do PC, ale można się szybko przyzwyczaić.

Klawiatura ma wbudowany dwa porty USB 2.0, więc można podłączyć bezpośrednio do niej dodatkowe urządzenie (np. myszkę). Porty są umieszczone na prawym i lewym boku klawiatury:

Ucieszył mnie przedłużacz USB. Pomyślałem, że przyda mi się do wyprowadzenia pojedynczego gniazda USB w jakieś dostępne miejsce. ZONK. Apple uznał, że przedłużacz ma pasować tylko do klawiatury ich firmy i zaprojektował małą modyfikację wtyczki:

Z czystym sumieniem mogę polecić taką klawiaturę wszystkim oczekującym wygody pisania.

goto

Ponieważ już nadeszły święta wypada życzyć licznej grupie naszych czytelników i miłośników wszystkiego najlepszego, zdrowych, szczęśliwych i pogodnych świąt.

Ponieważ jestem głodny a mucha zaczął mi opowiadać o jedzeniu (zła mucha!) a do tego nie mogę się doczekać prezentów (stęskniłem się za prezentem, który sobie sam kupiłem [przetestuję go dla Was jutro]) postanowiłem się poznęcać nad wami (głodnymi jak ja) pewnym obrazkiem:

Życzę wam, żeby takie coś jak na obrazku dodawali w przyszłym roku za darmo do porannej gazety… w sam raz na śniadanie. Na wigilię też by sie nadawało bo myślę, że ma więcej niż 12 składników. Policzmy:

• bułka
• sezam (na bułce)
• sałata
• ser
• cebula
• mięso wieprzowe
• sól
• pieprz
• majonez
• ketchup
• ogórek
• tłuszcz

Proszę: 12!!

Jeszcze raz: NAJLEPSZEGO!

goto

P.S. Oczywiście życzenia są od wszystkich moronów! Pauliny, Złej Muchy i Mnie!!!

Pisząc sobie dokument w latex’u spotkałem się z problemem natury estetycznej. Chciałem wstawić trzy małe rysunki do tekstu, co nie jest specjalnym wyzwaniem. Niestety rysunki te pojawiają jeden pod drugim i (mimo że są małe) zajmują, a właściwie marnują, ponad pół strony. Rozwiązaniem tego problemu jest wstawienie rysunków obok siebie. Jak tego dokonać? Są dwie drogi do sukcesu:

Droga 1:

Korzystamy z możliwości zagnieżdżania pudełek i stosujemy środowisko \minipage.

Do dyspozycji mamy 3 rysunki: AND.eps, OR.eps o NAND.eps:

\begin{figure}[h]
\begin{center}
\begin{minipage}[b]{4cm}
\centering
\includegraphics[width=4cm]{AND.eps}\\\textit{AND}
\end{minipage}
\begin{minipage}[b]{4cm}
\centering
\includegraphics[width=4cm]{OR.eps}\\\textit{OR}
\end{minipage}
\begin{minipage}[b]{4cm}
\centering
\includegraphics[width=4cm]{NAND.eps}\\\textit{NAND}
\end{minipage}
\caption{Bramki logiczne}
\label{bramki}
\end{center}
\end{figure}
W tekscie możemy odwołać się tylko do całego rysunku \ref{bramki}.

Po kompilacji dostajemy:

Wadą tego rozwiązania jest brak możliwości odwołania się do składowej części rysunku oraz konieczność definiowania szerokości środowiska \minipage.

Droga 2:

Korzystamy z pakietu subfigure. Należy pamiętać o dodaniu tego pakietu do dokumentu.

Teraz kod wygląda tak:

\begin{figure}[h]
\begin{center}
\subfigure[AND]{
\includegraphics[width=4cm]{AND.eps}
\label{AND}
}
\subfigure[OR]{
\includegraphics[width=4cm]{OR.eps}
\label{OR}
}
\subfigure[NAND]{
\includegraphics[width=4cm]{NAND.eps}
\label{NAND}
}
\caption{Bramki logiczne}
\label{bramki1}
\end{center}
\end{figure}
W tekscie możemy odwołać się do całego rysunku \ref{bramki1},
lub do składowych tego rysunku \ref{AND}, \ref{OR} i \ref{NAND}

A wynik tak:

Jak widać efekt jest podobny do poprzedniego. Zyskaliśmy jednak możliwość odwoływania się w tekście do składowych naszego rysunku.

goto

Jak niektórzy wiedzą, na urodziny została mi podarowana rybka (Goto, Paulina, Baśka – dzięki). Nie wiem co ta rybka im zrobiła – nieważne – dali ją mi. Można by właściwie powiedzieć że dostałem cały zestaw “Mały sadysta”.

Zestaw składa się z:

• Ośrodka nr.1 – Ośrodek jest sypki, masa około 500g, długość fali jaką odbija najlepiej to około 580nm (mówiąc nie po fizycznemu – żółty żwirek)
• Ośrodka nr.2 – Zapach, przezroczystość oraz gęstość wskazuje na wodę, ale nie wierzę, że goto niczego nie dosypał…
• Szklanego tak sądzę) tworu, nadającego więzy na położenie dla pozostałych elementów zestawu – r < R, gdzie R = 15cm.
• Klocka, który w zadaniach standardowo jest używany do zsuwania się po równi pochyłej, która zsuwa się po równi pochyłej, umieszczonej w wiadrze, które jest zawieszone na układzie 27 bloczków, całość dzieje się w jadącym po wykresie funkcji sinus wagonie wypełnionym miodem.
• Rybki właściwej

Niestety część zabawy została mi odebrana. Zestaw dostałem rozpakowany i zmontowany. Całość przedstawia się tak:

Początkowo rybka tymczasowo została nazwana dosyć popularnym w moim pokoju imienim “Maciek”. Doszedłem jednak do wniosku, że nie może tak być, że ktoś mnie woła a odwraca się ryba… Po paru dniach Maciek został przemianowany na Prosiaka. Od tej pory Prosiak grzecznie sobie żyje w moim akwarium i szykuje się do opisu tego co widzi… A widzi wiele! w końcu w jego pokoju mieszka dwóch fizyków i astronom… Ja bym na jej miejscu od razu zwariował. Swoją drogą, czy ta ryba nie została mi dana po to aby mnie kontrolować? Bo mam takie obawy.

Wraz z zestawem dostałem oczywiście karmę dla Prosiaka. Takie małe brązowe kuleczki. Spróbowałem – PFEEE!! No bez jaj, nie będę tym Prosiaczka mego karmił! Niestety nie znalazłem jeszcze odpowiednika. Wiem za to już czego Prosiak nie je. Otóż nie je:

• Fasolki
• Kanapek z boczkiem (nawet z majonezem!)
• Ziemniaków
• Karkówki w sosie cebulowo śmietanowy (Maćku, powinieneś się obrazić, mniamuśne było, a on nie chciał!)
• Maślanki

Obawiam się, że będę musiał się z Prosiakiem dzielić McRoyall’ami. Od razu odpowiem na nasuwające się pytanie – nie wrzucałem tego wszystkiego do akwarium (goto mnie przestrzegł: “Masz tam kurwa nic nie wrzucać!”). Grzecznie pytałem: “Te! Prosiak! kcesz kanapke? Z boczkiem, dobra jest. Nie? Posmaruje ci majonezem! Nie to nie, głodna kurwa pływaj!”

Wbrew pozorom zestaw ten uczy nie tylko odpowiedzialności, ale także cierpliwości. Do tej pory:

• Niczego tam nie dolałem (rozpałka do grilla, olej, Hoop-Cola… możliwości jest masę)
• Nie podłączałem jej do prądu
• Nie brałem jej do łap (no dobra raz, ale musiałem bo zmieniałem wodę…)
• Nie zjadłem jej

Na zakończenie dodam, że bardzo dobrze żyje mi się z Prosiakiem w pokoju. A najlepsze jest to że jest całkiem inteligentny, załapał już liczenie pochodnych a jutro przechodzimy do całkowania…

much.

P.S. Przepraszam że napisałem ten post. Jest trzecia w nocy… O tej porze człowiek nie myśli racjonalnie .

Halo (od greckiego hálos – tarcza słoneczna) – zjawisko optyczne zachodzące w atmosferze ziemskiej na kryształach lodu. Jest to świetlisty, biały lub zawierający kolory tęczy (wewnątrz czerwony, fioletowy na zewnątrz), pierścień widoczny wokół Słońca lub Księżyca. Część nieba wewnątrz kręgu jest wyraźnie ciemniejsza niż na zewnątrz. Zjawisko wywołane jest załamaniem na kryształach lodu i odbiciem wewnątrz kryształów lodu znajdujących się w chmurach pierzastych piętra wysokiego (cirrostratus) lub we mgle lodowej. Tak mówi wikipedia. A tak to wygląda:

Niestety to zdjęcie to ekstremalny przypadek. Uważa się nawet że jest to jedno z najbardziej spektakularnych i złożonych zdjęć halo. Połowy (a nawet większości) zjawisk widocznych na tym zdjęciu w życiu nie widziałem. Niektórych na pewno nie zobaczę, bo są ekstremalnie rzadkie. Najciekawsze jest to, że kilka zjawisk widocznych na zdjęciu (halo 22*, słońca poboczne, krąg parheliczny, górny łuk styczny i krąg okołozenitalny – które kiedy indziej opiszę czym to wszystko jest) jest bezproblemowo dostępna dla zwykłego człowieka. Ale i tak 90% ludzi nigdy tego nie widziało. Dlaczego? Po pierwsze ludzie nie patrzą (nie patrzycie…) w niebo. Popatrzcie czasami…. tych łuków to się można nieraz przestraszyć nawet. A nie są one wcale takie rzadkie. Najpospolitsze halo 22-stopniowe (czyli jasny świetlisty krąg o średnicy 22 stopni wokół słońca) to co kilka dni można zobaczyć. Nie raz utrzymuje się cały dzień.

Post ten jest takim małym wstępem. Niedługo zacznę się bardziej zagłębiać w opis zjawisk halo, mam nadzieję że kogoś do nich przekonam.

much.

Semestr 3 zaczął się już dawno, pierwsze kolokwia za nami, więc tekstów na marginesie trochę powstałoJ Postanowiłam podzielić się nimi wszystkimi bez wyjątków, bez cenzury, bez wybierania lepszych i gorszych. Każdy tekst ma swoją historie, ale z historią mogłyby stać się sensowne, a nie o to chodzi w tekstach z moich marginesów. Podzieliłam je na działy, bo lubię układać. Podział logiczny nie jest, ale mi umilił wklikiwanie tekstów na klawiaturze.

UWAGA ogólna czytając teksty NIE MYŚL o fizyce w żadnej formie, w żadnym wypadku, pod żadnym pozorem!

Zacznę od tych, kiedy to zastanawiam się „czy on naprawdę tak lubi mówić do siebie“. Są to chwile, kiedy prowadzący wykład lub ćwiczenia obraca się tyłem do tyłu i przodem do przodu, zasłania literki, krzaczki obrazki i inne…które umieścił już na tablicy i mówi słowa typu (przypominam o uwadze wstępnej):

„Omega kwadrat kwadrat minus gamma kwadrat omega kwadrat kwadrat” mismap główkuje aż mu się tam oporniczki w mózgu grzeją natomiast dla osoby niemyślącej o fizyce w żadnym sensie brzmi to mniej więcej tak… jak brzmi, jeśli zastosowaliście się do uwagi.

Innym razem zamyślony powiedział:

„No… tylko, co ja właściwie liczę…” Nie odpowiedzieliśmy…

Czasami prowadzący mówią żarty, czasami śmieszne, czasami nie wiedzą, że mówią coś śmiesznego:

„To każdy sobie może policzyć…”

Są też chwile, kiedy chce się podpowiedzieć lub dopowiedzieć coś prowadzącemu:

• „-to po ro to po ro” „-Toporem“. Nie napisze, co robiłam w tym momencie tym ostrym narzędziem w swojej wyobraźni.
• „siedzi w kole” „-i macha nóżkami” (powoli wiecie jak pracuje mój musk na zajęciach…)

Do rozbudowy tego działu potrzebna mi będzie wasza pomoc.  

Rozmowy prowadzących i studentów

• widzicie? -(szeptem) na pewno Pan tam palcem popycha z góry… -są tak małe że można tylko palcem wyczuć. Czuję to palcem! Kto chce może podejść i dotknąć…
• bo rysunek był kiepski -no to trzeba było zrobić następny –A no to nie wiedziałem że mogę się tak wozić
• umiemy rozwiązać takie równanie? -Zostaliśmy poinformowani, że wychodzi SYF :/
• …związać się z jedną kulą -no wiążemy się. Są różne więzi…
• (szeptem) kropki jeszcze – (przerażony) Gdzie kropki, gdzie!?!
• Powiedzieć skąd się to bierze? -Nie!
• (zadowolony)A niedługo już zadanie 32! –no i co? – no jak to! Przecież 32 o potęga 2!

Powiedziane

• „Pierwiastkować może pan metodą dopisania”
• „no to wiadomo… że tam… sinus to jest z grubsza cosinus czy coś tam…
• „wrrr… powietrze nie lubi”
• „nie wymagam od was tego, ale to jest trywialne”
• „uwzględnienie rotacji jest karkołomne”
• „ja nie będę pisał tego, ale przypomnijcie sobie ze SZKÓŁKI”
• „potrenujcie trochę tego Google’a”
• „to jest takie o: (tu wsadził i wyciągnął mały palec z ust) z palca wyssane”
• „zero wybieramy w sposób… INTELIGENTNY. To jest arcyważne!”
• „teraz zrobimy to jak czołgiści a później będziemy jak motylek”
• „to teraz finezyjnie, czyli jak motylek”
• „stosujemy taki TRIK… chociaż „trik” to dużo powiedziane… Ale niech będzie! TRIK! Sztuczka!”
• „x,y to był nasz wybór mogliśmy wybrać a i ą, ś, ć”
• „to jest jakiś mismap albo inne cholerstwo”
• „ta siła nam tu silniej znika” (przp. Uwaga wstępna)
• „Wyobraźmy sobie model szczura w postaci jednorodnej kuli o gęstości r”
• „Fizyka wszystko potrafi sprowadzić do brutalnych równań… Takie poetyckie słowo <>”
• „skoro ona jest nieważka to jest nieważna, mała. Nie można pisać jej przez duże L”
• „znaczy nie to, że Bohr miał atom, tylko chodzi o model”
• „papier lepiej kleić, materiał lepiej szyć”
• „każde dziecko wie, że det odwzorowania jest odwrotnością tego odwzorowania do którego to odwrotne jest no.. odwrotne”
• „każde zadanie można TAK rozwiązać: „dla bardzo małych chwil nic się nie dzieje””
• „teraz szybciutko przelecimy kolokwium”
• „to taki kopniak jak zderzenie kulek”
• „małe „r” MUSI być większe od dużego „R””
• „to zapraszam do tablicy… oczywiście to nie przez to Pana spóźnienie”

Teksty z marginesów własnego autorstwa:

• chyba… tylko chyba wiem dlaczego
• zauważ że jednostki się zgadzają
• to się odbije po prostu
• może 3 może nie
• a później profesor przez 20min brzdąkał na gitarze(która nie była nastrojona)
• do biegunowych i komu się nudzi niech liczy całkę
• tutaj się spóźniłam bo jadłam obiad
• myślisz o czymkolwiek innym niż seksie? -taak! O grze wstępnejJ
• sru tu tu tu kawał drutu jednowymiarowego
• (przy pokreślonych przeliczeniach) nie liczyłam tego sama tylko przepisywałam te bzdury z tablicy żeby dojść do wniosku, że skorzystamy z gotowych wyników ;/
• ZzZzZzZzZzZzZzZzZzZzZzZzZzZzZzZzZzZzZzZzZzZzZzZzZzZz…

i w tej dziedzinie: wykład 1 fizyka III – wnioski i przestrogi na przyszłość:

• musze czytać książki bo na wykładach są pokazy
• musze umieć na ustny to czego nie umiałam na pisemny
• „róbcie wszystko żeby studiowanie było przyjemnością” – kulki(cząsteczki) są z czekolady

Usłyszane rozmowy kolegów i własne:

• -jakbym usiadł koło Muszki to bym się poprzytulał -to się zamieńmy (zamienianie się jest fajne)
• nie ma złudzeń. Photoshop!
• -osiem oczek ma ta kostka, tak? – Ty masz dwa i Ci więcej nie wyrośnie!

I na koniec. Prowadzący „rysuję nowe zadanie”: równia na sprężynce, masa na równi… na to student z ławki pyta: „A gdzie jest kondensator?”

Paulina (trzeci moron, a właściwie pierwsza moronka)

Ponieważ w komentarzu do mojego posta o zadaniach dla humanistów pojawiła się kwestia obliczeń numerycznych w programie Mathematica, napiszę o tym teraz.

Gdy próbujemy policzyć w Mathematice prostą rzecz typu:

In: 4*Sqrt[17] + Sin[Pi/5]

Otrzymamy nieciekawe wyrażenie:

Out: 4 Sqrt[17] + Sqrt[5/8 – Sqrt[5]/8]

Zapisując w sensowny sposób nasz wynik wygląda tak:

Ale ile to jest? Użycie opcji Simplify lub FullSimplify nie daje efektu, tego wyrażenia nie da się (zdaniem Mathematici) bardziej uprościć.

Aby otrzymać wynik musimy poprosić Mathematicę o wynik numeryczny poprzez zastosowanie opcji N

Gdy tak zrobimy otrzymamy wynik:

In: 4*Sqrt[17] + Sin[Pi/5] // N
Out: 17.0802

Otrzymaliśmy wynik numeryczny. Może się jednak zdarzyć, że dokładność wyniku nie jest dla nas zadowalająca. Należy wtedy skorzystać z N w trochę innej postaci:

In: N[4*Sqrt[17] + Sin[Pi/5],50]
Out: 17.080207754763115328454345378535380869186449339138

Gdzie drugim argumentem N[] jest liczba cyfr znaczących w wyniku.

goto

Ponieważ (ku ogólnemu zdziwieniu) istnieje na II roku wydziału fizyki przedmiot, który mamy szansę zaliczyć na więcej niż 3 (zresztą zazwyczaj dawane, żeby nas więcej nie oglądać) postanowiliśmy się nim trochę bardziej zainteresować. Chodzi rzecz (kurwa, czemu ja napisałem rzecz przez “ż”?) jasna o elektronikę. Na przedmiocie tym zajmujemy się elektroniką cyfrową i analogową.

Na pierwszym ćwiczniu mieliśmy do czynienia z układami scalonymi serii 74. Fascynujące było jak połączone drucikami (druciki to kabelki zakończone ostrym wtykiem. Twórcą kabelków jest Pani Grażynka, która miała cierpliwość zrobić setki kabelków w czasie wakacji – podziwiam) kilka scalaczków realizuje zamierzoną logikę.

Ponieważ na następne ćwiczenie szykowała się elektronika analogowa (wzmacniacze) i robienie (za razie ręczne) kilkuset pomiarów właściwie tego samego, tylko po to żeby narysować wykres nie wnoszący niczego odkrywczego postanowiliśmy wziąć sprawy w swoje ręce. W naszym laboratorium podpatrzyłem (dzięki uprzejmości Pana Andrzeje – pozdrawiam) układ elektroniczny z programowalnym mikrokontrolerem. Szybko okazało się, że owy układ to gotowa płytka uruchomieniowa do tegoż mikrokontrolera (ideą takiej płytki jest umożliwienie łatwej konfiguracji sprzętowej takiego mikrokontrolera. Ponieważ łatwo się wszystko podłącza można sie skupić na nauce pisania programów na taki mikrokontroler).

Po małym przeszukaniu internetu szybko zdecydowałem się na zestaw uruchomieniowy ZL3AVR wydawnictwa BTC. Sercem tego zestawu jest mikrokontroler ATmega32 firmy ATMEL (o samym chipie następnym razem).

Zestaw (gotowy do uruchomienia) można kupić na stronie producenta: http://www.kamami.pl/?id_prod=10502 za jedyne 329 zł… sporo. Okazuje się, że za 49zł można kupić samą płytkę drukowaną i samemu zmontować.

Podzieliłem się pomysłem z muchą, a ten oświadczył, że on też chce mieć taki zestaw i że w ogóle to nie ma dyskusji bo on chce. Jak chce to ok. Zdecydowaliśmy się na zakup płytki i samodzielny montaż. Wypisałem ze schematu jakie elementy musimy kupić i pojechaliśmy na zakupy. Niestety okazało się, że w warszawie da się kupić tylko 1 płytkę (w sklepie na wolumenie). Kupiłem ją dla siebie (tak, wiem że jestem samolubny, ale jestem jedynakiem i mam takie prawo. Mucha jedynakiem nie jest więc musiał się ze mną podzielić… takie życie), a drugą dla muchy zamówiliśmy i czekamy. Trzeba było dokupić wszystkie potrzebne elementy (lista elementów następnym razem). W sklepie na wolumenie się nie udało bo sprzedawcy się nie chciało kompletować elementów. Jego strata. Pojechaliśmy na Hożą i kupiliśmy prawie wszystko (brakowało paru nieistotnych elementów). Mimo braku płytki muchy postanowił on kupić od razu elementy dla siebie. W sumie wszystko kosztowało (płytka, elementy i zasilacz) około 200 zł. Do tego musiałem później dokupić nietani (70zł) programator, ale o nim następnym razem.

Wróciłem z tym wszystkim do domu (strasznie podniecony nadchodzącym lutowaniem) i zabrałem się do pracy:

o 18:46 miałem na stole takie coś:

robiłem przerwy i szło mi powoli, bo do 20:29 zrobiłem niewiele:

potem szło mi lepiej bo 9 minut po północy skończyłem:

Następnego dnia kupiłem programator i napisałem swój pierwszy program na mikrokontroler ATmega32, ale o tym następnym razem.

Ponieważ o wielu rzeczach obiecałem napisać następnym razem, następnych razów zdecydowanie będzie kilka. Może do tego czasu mucha dostanie swoją płytkę?

goto