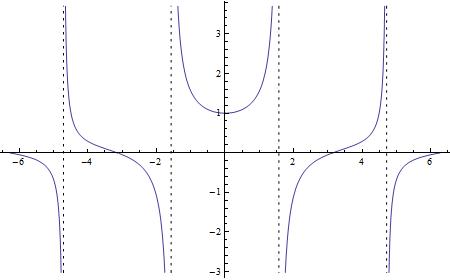
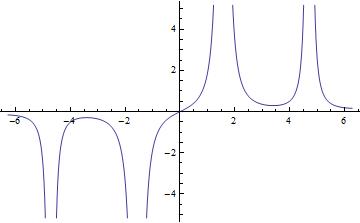
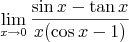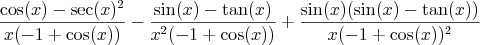Jak już wspominałem wcześniej, 26 października odbyło się od dawna wyczekiwane kolokwium z mechaniki klasycznej A. Brać studencka albo trzęsła portkami już na tydzień wcześniej nie wiedząc czego się spodziewać albo po prostu miała to kompletnie w dupie, dochodząc do wniosku, że chyba czas rzucić studia. Ja się przyznam. Uczyłem się. Skopiowawszy uprzednio wraz z Goto notatki (sztuk cztery) Maćka mojego współlokatora (pozdrawiam), zasiadłem w weekend do nauki. A nie było to łatwe, gdyż po imprezie która odbyła się pod naszymi drzwiami (Takie coś znalazłem w łazience o 2 w nocy) Wszystkie nasze krzesła wyparowały. Nauka na głośniku była średnio wygodna, tak więc po przemyśleniu wszystkich za i przeciw udałem się do pokoju cichej nauki. I nie chce tego komentować… to było z mojej strony głupie – przepraszam…

…7:00 – utwór na trąbce z filmu Kill Bill oznajmia mi, że czas wstawać… Grając coraz głośniej przypomina mi jak dawno nie wstawałem o tej porze. Szybki prysznic, maślanka, Turbo-Bronsztein do plecaka (wyjaśnię co to kiedy będę szedł przez pola mokotowskie). Jakiś papier długopis i już z Maćkiem na Smynie targamy… a nie jest to proste logistycznie. Najpierw 10 min idziemy przez pola, tak więc mam chwilkę aby opowiedzieć co to Bronsztein. Bronsztein (Matematyka, poradnik encyklopedyczny, I.N.Bronsztein, K.A.Siemiendiajew) to Biblia fizyków. Jest tam wszystko. 50 stron tablic całek, triki, dzięki którym równania różniczkowe stają się proste jak metr drutu w kieszeni. po prostu cud książka. A najlepsze jest to, iż można z niej korzystać na kolosach i egzaminie z mechaniki!. Turbo-Bronsztein to specjalna odmiana Bronszteina, o której publicznie mówić nie wolno… Po dojściu do metra, jedziemy kilka przystanków, potem trambaj, piechotką kilkaset metrów i jesteśmy na smyniach. Gdy przekroczyłem próg, coś mnie połaskotało… taki sentyment… jak ja dawno tu nie byłem! Ostatnie przed kolokwialne rozmowy… wymiana uwag… no i piszemy

…8:30 – Usadowiliśmy się, dr. Rafalski nas przetasował, kartki rozdano… rzut oka na zadania – ooo nie jest źle… pierwsze zadanie – zrobiłem… Drugie… zacząłem… i się zawiesiłem… Trzecie – za cholerę. Było kilka sposobów na zrobienie tego zadania. Można było tak jak ja probować coś policzyć, co było złą drogą. Można też zrobić tak jak Goto. Rozpiździć zadanie po całej kartce, niech kombinują, a nuż sami coś wymyślą że jest dobrze.

…10:45 – ludzie zaczynają wychodzić… goto wyszedł… no to co będę siedział jak kretyn? Minęło pół godziny i już z Pauliną, Baśką i Goto, testujemy w Smyczkowym Maczku podwójne McRoyalle.. mmm cóż to za kanapka… 2000 Kcal… nie ma to jak pocieszenie po walce z zadaniami…

…Much

W zeszłym tygodniu miałem okazję odwiedzić i zwiedzić Instytut Problemów Jądrowych im. Andrzeja Sołtana w Świerku pod Warszawą. Najciekawszym, rzecz jasna, punktem programu było zwiedzanie jedynego w Polsce, czynnego reaktora jądrowego “Maria” (reaktor ten powstał w latach 70-dziesiątych i od tamtej pory pracuje wyłącznie do celów naukowych – nie jest produkowana w nim energia elektryczna). Zdjęcia z wewnątrz budynku reaktora (+ parę innych) umieściłem w swojej prywatnej galerii zdjęć.

Niestety po przekroczeniu bramy ośrodka stajamy się świadkami bardzo smutnego faktu: bieda. Pracuje tam wielu wspaniałych naukowców (miałem okazję posłuchać tylko kilku niestety), których (w moim przekonaniu) potencjał marnuje się przez przestarzałą aparaturę i brak środków na badania. Świat w Świerku wydaję się być wierną kopią PRLu. Jak ktoś by chciał nakręcić film osadzony w realiach PRLu to w Świerku sceneria jest gotowa i czeka.

Jeszcze raz zapraszam do oglądania zdjęć.

Mały apel do polityków (właściwie dwa): Dajcie więcej pieniędzy na naukę i ruszcie z budową prawdziwego, komercyjnego reaktora w Polsce. To jest na prawdę tanie i zdrowe źródło energii!

goto

Witam wszystkich po przerwie paro dniowej (wiem, że pisałem nie tak dawno, ale światło przez ten czasu uleciało daleko a ja nie).

Postanowiłem sobie kupić tablet graficzny co bym mi się łatwiej rysowało rysunki do zadań i żebym mógł naszkicować muchę. Mały research, pytanie na grupę dyskusyjną i dowiedziałem się że tak na prawdę tylko tablety firmy Wacom są warte polecenia. Obejrzałem ofertę i wybrałem (Bamboo A6 – 3 od dołu pod względem ceny) tablet o powierzchni roboczej wielkości A6. Zerknąłem na “gdzie kupić” i postanowiłem się wybrać do Media Markt’u.

W sklepie sprzedawca przekonał mnie, że nie ma sensu kupować Wacom’a za ponad 300 zł do takich zastosowań jak ja potrzebuję (Wacoma i tak nie było). Polecił Pentagrama (O`pen XL USB) mówiąc, że studenci architektury są zadowoleni. No dobra. 2 razy większa powierzchnia robocza (A5) i 2 razy mniejsza cena (169 zł). Kupiłem.

Wróciłem do domu rozpakowałem, zainstalowałem sterownik podłączyłem…. działa. Obsługuje się to dziwacznie, ale można się przyzwyczaić (Powierzchnia A5 to za dużo. A6 byłoby zdecydowanie lepsze). Postanowiłem coś narysować. Efekt koszmarny. Jakieś bazgroły krzywe a nie rysunek. Doszedłem do wniosku że coś jest nie tak. Sięgnąłem szybko po linijkę, aby przy niej narysować prostą. Pozioma ok (nie licząc zakrzywienia na brzegu). Pionowa ok. Narysowałem po skosie…. ło boże……

Poniższy rysunek przedstawia kilka “prostych” rysowanych przy linijce:

Spakowałem to badziewie od razu du pudełka i pojechałem do Media Markt oddać. Pani zaproponowała mi wymianę na taki sam model. Oj nie… ja dziękuję… Dostałem zwrot pieniędzy i kupiłem sobie blender 🙂

Morał: Pentagram jest beee

goto

Każdy fizyk wie, że świat dookoła najłatwiej opisać równaniem różniczkowym. Reszta (“czyli większość pozostająca w opozycji”) zapewne nie wie, że wzory (np. na ruch wahadełka czy słynnej masy na sprężynce) wypisywane na ściągach w liceum i wcześniej są rozwiązaniami równań różniczkowych opisujących dany problem.

Z powyższego powodu (gloryfikacja równań różniczkowych) chciałbym napisać parę prostych przykładów rozwiązywania równań różniczkowych za pomocą programu Mathematica.

Ponownie sięgnę po zadanie z kolokwium z I roku. Mamy do rozwiązania równanie różniczkowe:

Niezbyt skomplikowane równanie pierwszego rzędu… dałoby się policzyć nawet w pamięci, ale po co?

Prosimy Mathematicę o rozwiązanie:

In: DSolve[x^2 y'[x] == (y[x])^2 + x y[x], y[x], x]
Out: y[x] -> x/(C[1] – Log[x])

Trochę wyjaśnienia o funkcji DSolve. Przyjmuje ona 3 argumenty: równanie (lub równania, o czym zaraz), funkcję jakiej rozwiązania szukamy oraz zmienną niezależną. W naszym przypadku interesuje nas rozwiązanie postaci funkcji y(x), gdzie x jest zmienną niezależną. Przy zapisywaniu równań należy pamiętać że y jest funkcją x (nie piszemy y” tylko y”[x]).

Mathematica zwróciła nam rozwiązanie ogólne:

W zadaniu poproszono nas jeszcze o rozwiązanie tego równania różniczkowego z uwzględnieniem warunku początkowego:

Możemy to zrobić na 2 sposoby:

• Podstawić x=1 do rozwiązania ogólnego i rozwiązać równanie na stałą C1

In: Solve[1/(C1-Log[1])==1,C1]
Out: C1 -> 1

• Uwzględnić warunek początkowy przy rozwiązywaniu równania poprzez DSolve (jako pierwszy argument podajemy dwa równania ujmując je w klamry {} i oddzielając przecinkiem):

In: DSolve[{x^2 y'[x] == (y[x])^2 + x y[x],y[1]==1}, y[x], x] //Simplify
Out: y[x]->x/(1-Log[x])

Jak widać obydwie metody prowadzą nas do tego samego wyniku:

Przy bardziej skomplikowanych równaniach mających więcej warunków początkowych druga metoda okazuję się być zdecydowanie bardziej efektywna.

Ostatnią rzeczą o którą prosił nas autor jest narysowanie otrzymanego rozwiązania:

In: Plot[x/(1 – Log[x]), {x, 0, 6}, {Exclusions -> {1 – Log[x] == 0},
ExclusionsStyle -> Dashing[Small], PlotRange -> 50}]

Otrzymujemy:

Tak więc wiemy już jak zabrać się za rozwiązywanie nieskomplikowanych równań różniczkowych. Następnym razem pobawimy sie macierzami

goto

Jako przedstawiciel astronomicznej części fizyki na tym blogu, czuję się zobowiązany do napisania o niesamowitym zjawisku jakie widzimy od jakiegoś czasu na naszym niebie. Chodzi o kometę 17P/Holmes, która zarówno zaskoczyła zarówno zawodowych astronomów, jak i zwykłych oglądaczy nocnego nieba.

Ta kometa to kupka śniegu o średnicy około 3 km…

Zacznijmy od początku. Kometę odkrył przeszło 100 lat temu Edwin Holmes – brytyjski astronom, podczas obserwacji jednej z najpiękniejszych galaktyk na naszym niebie – M31 w andromedzie. Była wtedy ona wystarczająco jasna by można ją było zobaczyć gołym okiem.

Orbita komety, czyli tor po którym się ona porusza ma kształt średnio spłaszczonej elipsy. W pobliże słońca wraca mniej więcej co 6 lat. Dwa tygodnie temu była jeszcze słabiutkim obiektem o jasności około 17mag, co znaczy że interesowała jedynie zawodowych astronomów, jeżeli w ogóle kogoś interesowała. I tu stała się rzecz niesłychana. Jasność gwałtownie wzrosła do 3mag… Dla niewtajemniczonych napiszę, że wzrost jasności z 17 do 3 mag oznacza około milionowe pojaśnienie… Kometa wysyła teraz MILION razy więcej światła niż 2 tygodnie temu. To największy wzrost jasności komety w tak krótkim czasie w historii (największy zarejestrowany). Pojawiły się spekulację, iż kometa w coś przypierdzieliła. Nie jest to jednak prawdopodobne, gdyż wcześniej (te 100 lat temu) odnotowano podobny wybuch, i dzięki temu ją odkryto. Choć nie wiedziano wtedy że był to wybuch.

Czy jest jeszcze coś ciekawego w tym zjawisku? Ano jest. Zdecydowana większość komet osiąga maksymalną jasność podczas największego zbliżenia do słońca. Kometa jest to taka kupa brudnego śniegu latającego sobie w przestrzeni. Gdy zbliża się do słońca śnieg zaczyna sublimować i ulatywać w przestrzeń tworząc ogon. Powoduje to też silniejsze świecenie (ogólnie i skrótowo mówiąc by nie zanudzać). Obserwacje są wtedy jednak trudne, gdyż ponieważ gdy kometa jest blisko słońca to jest blisko słońca (wiem.. brawurowe jest to zdanie). A gdy nad horyzontem jest słońce to mamy dzień i astronomowie idą spać bo komet NIE WIDAĆ… 17P/H zrobił natomiast wszystkich w wała, dostając energetycznego kopa, wtedy gdy jest od słońca daleko. I widać ją przez całą noc, dzięki czemu na niebie mamy całkiem ładne widowisko, choć nie jest to wygląd typowy dla komety. Ogólnie mówiąc, wygląda ona jak całkiem jasna gwiazdka, którą ktoś rozmazał palcem. Ciapka wśród mrowia kropek. Zachęcam do zwrócenia na nią uwagi, gdy tylko pogoda sie odobrazi i przestanie walić żabami…

Na koniec dodam, że kopiąc po necie za informacjami na temat kometki kilka dni temu, Trafiłem też na pewne forum dotyczące różnych paranormalności, na którym natrzaśnieci lekko ludzie, szukają we wszystkim końca świata. Nie mając zielonego pojęcia o ruchu ciał niebieskich pierdolą głupoty wkręcając się nawzajem. Twierdzą, iż ponieważ nie widać ogona który “musi” (kretyni) mieć każda kometa tak więc z całą pewnością kometa leci w stronę ziemi którą to oczywiście rozpieprzy. (Swego czasu była na tym forum niesamowita akcja o pewnej komecie, którą na pewno tu opiszę.) Dla uspokojenia czytelników informuję co następuje:

• komety posiadają 2 warkocze – gazowy i pyłowi skierowane w różne strony. Żaden nie musi być widoczny.
• Warkocz gazowy nie podąża za kometą, tylko jest skierowany w kierunku przeciwnym do słońca.
• Żadne ciało niebieskie nie porusza się po linii prostej. To znaczy że nawet jakby chwilowo prędkość komety była skierowana w Ziemię to i ona i Ziemia zaraz się rozjadą

Pozdrawiam, i zachęcam do obserwacji póki jeszcze mamy szansę.

Much

Niektóre teksty wypowiedziane przez naszych wykładowców są tak niestandardowe, że nie można ich pominąć w swoich notatkach.

Nasza koleżanka Paulina wynotowuje co ciekawsze sentencje i zapisuje na marginesie. Oto co udało jej się zapisać na początku I roku studiów:

“Gdy mamy stale napięcie no to wtedy musimy powiedzieć ze mamy stale napięcie.”

“Czy to „B” nie mogłoby mieć jakichś brzuszków”

“Bardzo skończony wielomian równy 1”

“Jak dużo? mało dużo, mnóstwo, okropnie dużo, …”

“Okropnie kształcący przykład”

“Gdybyśmy mieli baaardzo dużo wolnego czasu to pewnie byłoby pasjonujące zajęcie”

“Strzałka za przeproszeniem”

“Dowód to policzenie co wymaga tylko zużycia pewnej ilości kredy”

“To taka definicja składająca się z pobożnych życzeń – gdybyśmy go znaleźli to byśmy się cieszyli”

“Zdarzają się czasem na świecie takie przypadki ze pochodna jest liczbą i tu taki wziął i przyszedł”

“(…) oparte chyba na prawie Newtona … bo (to) jest chyba prawo Newtona…”

“3/4 punktów za to ze nic nie zrobiłem źle” (usłyszane na korytarzu)

“niektóre nowe mogą być stare”

“pochodna istnieje i znika”

“kąty mówią coś o kierunkach a z wszystkich kierunków powinno zmierzać… wiec zależy od kierunku, granica nie istnieje”

Tylko proszę, nie pytajcie co autorzy tych wypowiedzi chcieli przekazać studentom, bo ja też nie wiem.

goto

Znalazłem dzisiaj za biurkiem zeszłoroczny egzamin z analizy I C. Postanowiłem się pobawić Mathematicą i porozwiązywać zadania nie wysilając własnej szarej komórki.

Ponieważ to część pierwsza przykłady będą banalne, ale dające ładne efekty 🙂

Poniżej podzielę sie wnioskami z rozwiązywania drugiego przykładu z piątego zadania za pomocą programu Mathematica. Zadanie da się rozwiązać od razu więc nadprogramowo się nim pobawimy (a co za tym idzie pobawimy się Mathematicą, a na tym najbardziej nam zależy).

Zadanie: należy obliczyć następującą granicę:

Nic prostszego! Na początek zdefiniujmy sobie funkcję, której granice będziemy liczyć:

In:= k[x_] = (Sin[x] – Tan[x])/(x (Cos[x] – 1))

Teraz możemy przeprowadzać różne operacje na tej funkcji. Policzmy granicę, o którą pytają nas w zadaniu:

In:= Limit[k[x], x -> 0]
Out:= 1

Jak widać granica tej funkcji przy x dążącym do zera wynosi 1.

Niby rozwiązaliśmy zadanie, ale mnie nadal ciekawi jak ta funkcja wygląda (te trygonometryczne zawsze są ładne). Narysujmy więc:

In:= Plot[k[x],{x,-2*Pi,2*Pi}]

Jako wynik otrzymujemy wykres:

Funkcja ładna, rzeczywiście dąży do 1 dla x dążącego do 0, ale wykres jeszcze nie bardzo. Poprawmy te pionowe krechy (poprzez wyłączenie punktów krytycznych z wykresu):

In:= Plot[k[x],{x,-2*Pi,2*Pi}, {Exclusions -> {Tan[x] == 0}}]

Otrzymujemy:

Już ładniej, ale zrobiło sie trochę “łyso”. Przydałyby się asymptoty:

In:= Plot[k[x],{x,-2*Pi,2*Pi}, {Exclusions -> {Tan[x] == 0}, ExclusionsStyle -> Dashing[Small]}]

Otrzymujemy:

Teraz otrzymaliśmy (przez zastosowanie dwóch opcji) bardzo ładny wykres funkcji z zadania.

Funkcje mające ładne wykresy mają zazwyczaj ładne pochodne. Ta nie jest wyjątkiem. Obliczamy pochodną funkcji po x:

In:= D[k[x],x]

Mathematica zwraca nam przepiękny wzór na pochodną naszej funkcji:

Który po uproszczeniu (polecenie Simplify[]) przyjmuje następującą postać:

sec to secans, czyli stosunek przeciwprostokątnej i przyprostokątnej przyległej do kąta ostrego a więc odwrotność cosinusa.

Narysujmy sobie jeszcze tą pochodną:

In:= Plot[{(x Sec[x]^2 – Tan[x])/x^2}, {x, -2*Pi, 2*Pi}]

Otrzymany wykres wygląda następująco:

Ładny, prawda?

goto

Przyszło mi dzisiaj napisać pierwszy wpis o tematyce wyłącznie politycznej. Sytuacja ku temu jest dzisiaj bardzo dobra, a to ze względu na fakt zaprzysiężenia nowego sejmu i senatu.

Niestety na nowy rząd, który w moim przekonaniu będzie nieporównywalnie sprawniejszy i bardziej merytoryczny od poprzedniego rządu koalicji PiS’u z LPRem i Samoobroną trzeba będzie parę dni poczekać. Rozumiem, że są tacy, którzy się ze mną w powyższej kwestii nie zgadzają. Nie rozumiem jednak co tacy ludzie widzieli pozytywnego w rządzie Jarosława Kaczyńskiego i w tej kwestii zapraszam do merytorycznej dyskusji.

Nie chcę dzisiaj pisać na temat poprzedniego rządu (szkoda nerwów moich i waszych). Jestem zdania, że nie należy rozpamiętywać przeszłości, tylko należy (a nawet trzeba) patrzeć w przyszłość. Było co było i nic tego nie zmieni. Szkoda tylko, że zostały Polsce zmarnowane kolejne dwa lata.

Szkoda, że PiS nie jest w stanie wyciągnąć żadnych wniosków z wyborów. Szkoda, że nie rozumieją obywatelskiego NIE patrzeniu na każdego jak na złodzieja, pedofila i anty patriotę. Naprawdę szkoda.

Mimo, że wybory za nami nadal słucham w mediach propagandy PiS’u, który zapowiada, że będzie patrzył Platformie Obywatelskiej na ręce, bo PO to “złodzieje którzy rozkradną i sprywatyzują całą Polskę”. Chciałbym, aby były premier Jarosław Kaczyński zrozumiał: wybory już były i PiS je przegrał. Teraz rządzi kto inny, a PiS nie jest i nie będzie organem kontrolującym pracę rządu.

Kolejnym tematem wartym poruszenia w tak szczególny dla Polskiej polityki dzień jak dzisiaj jest “barwna” postać Prezydenta. Prezydent tak bardzo nie może się pogodzić z porażką swojego brata, że nie przemawia na inauguracji nowego sejmu? To nie jest nawet śmieszne…. to jest żenujące! Panie Prezydencie: Europa i świat się z nas przez Pana śmieją!!! Nie do pomyślenia jest, że Prezydent może nie pogratulować liderowi zwycięskiej partii. Nawet jak się kogoś szczerze nienawidzi trzeba zacisnąć zęby i uścisnąć dłoń!!!

Zachowanie Pana Prezydenta przypomina mi zachowanie kilkuletnich dzieci bawiących się w piaskownicy: “Mamusiu, ja go nie lubię bo on jest be i zabiera mi moje zabawki! Nigdy się do niego nie odezwę!”. Widzicie podobieństwo?

Nie będę pisał więcej bo zaczną mnie ponosić emocje, a to jest niewskazane.

Nie jest wielką tajemnicą, że do tematu “sytuacji politycznej” będziemy z muszką wracać.

goto

P.S. na wszelki wypadek jeszcze przeproszę Pana Prezydenta.

Poprzednim razem starałem się opowiedzieć jakie (moim skromnym i zazwyczaj niewiele znaczącym zdaniem) oprogramowanie można uznać za niezbędne na komputerze każdego przyzwoitego fizyka. Jednak komputer to nie wszystko. Trzeba umieć sobie poradzić z obliczeniami “w terenie” czyli na zajęciach (oczywiście można nieraz brać ze sobą komputer, co czasami czynię, lecz nie jest to rozwiązanie zbyt ergonomiczne [mimo, że mój laptop jest naprawdę leciutki i malutki])…

Reasumując: każdy szanujący się fizyk winien posiadać kalkulator!

Chciałbym przedstawić teraz w krótkim opisie dwa różne kalkulatory – jeden zaawansowany i drugi wypaśnie zaawansowany. Z pierwszego korzystałem do końca nauki w liceum. Drugi nabyłem (na miejsce pierwszego) wraz z rozpoczęciem studiów na Wydziale Fizyki UW.

• Kalkulator zaawansowany:

Poniższa recenzja będzie dla kalkulatora krzywdząca. Będę pisał o jego wadach nie wspominając, że umiałem wykorzystać mniej niż parę procent jego wielkich możliwości.

W liceum korzystałem z kalkulatora Casio fx-6300g. Zaawansowan, mały, lekki, poręczny kalkulator. Jego zdecydowaną wadą był mały ekran graficzny, na którym ciężko było dostrzec rysowaną funkcję oraz brak zapisu w notacji normalnej, co powodowało, że znalezienie błędu w tasiemcowym zapisie było zdecydowanie wyzwaniem.

Do wad należy zaliczyć również brak funkcji liczenia pochodnych i rozwiązywania całek nieoznaczonych (o równaniach różniczkowych niewspominając).

Casio fx6300g:

Podsumowując: poleciłbym ten kalkulator wszystkim poszukującym urządzenia do wykonywania średnio skomplikowanych operacji numerycznych.

• Kalkulator wypaśnie zaawansowany:

Podobnie jak poprzednio poniższa recenzja może być dla kalkulatora krzywdząca a to ze względu na fakt, że umiem wykorzystać mniej niż parę procent jego wielkich możliwości.

Zaczynając studia na Wydziale Fizyki postanowiłem wyposażyć się w “porządny” kalkulator. Przejrzałem ofertę i wybrałem kalkulator TI-92 Plus firmy Texas Instruments.

Nie jest to konstrukcja najnowsza, bo pochodzi pochodzi z 1998 roku. Firma Texas Instruments wypuściła w 2002 roku następcę tego modelu (Voyage 200). Nowy model ma zmniejszone gabaryty i zwiększoną do 2,7MB ilość pamięci (oba modele mają tyle samo RAMu). Wybrałem poprzedni model ze względu na fakt, iż kosztował połowę tego co jego młodszy brat.

Troszkę o kalkulatorze: jest ogromny (co nie jest jego zaletą jeżeli chodzi o transport w torbie). Otrzymujemy za to potężny wyświetlacz graficzny (240×128 pikseli) i pełną klawiaturę alfa numeryczną (plus oczywiście klawisze niezbędne do szybkiej i intuicyjnej obsługi kalkulatora). TI-92 Plus oprócz dokonywania obliczeń o dużej precyzji potrafi:

• rozwiązywać równania i układy równań
• operować macierzami
• liczyć pochodne i całki (chociaż nie zawsze radzi sobie z całkami Sołtanowskimi)
• rozwiązywać równania różniczkowe z uwzględnieniem warunków początkowych
• rysować wykresy funkcji i wykresy parametryczne
• rysować wykresy 3D funkcji dwóch zmiennych
• operować tabelami danych (potrafi nawet narysować histogram)
• upraszczać i przeliczać jednostki fizyczne w równaniach
• zapisywać równania i obliczenie w notacji normalnej (czytelniej dla stworzenia człekokształtnego)
• oraz wiele wiele innych (z czego większości jeszcze pewnie nie odkryłem)

W oknie głównym na wyświetlaczu kalkulatora widzimy ostatnie 99 obliczeń i możemy z każdego z nich skorzystać w kolejnym równaniu. Możemy również podzielić ekran na dwie części: na jednej mieć obliczenia a na drugiej wykres.

Możliwości tego kalkulatora są równie wielkie jak on sam. Można go nawet podłączyć do komputera i wgrać mu dodatkowe oprogramowanie (nie będę o tym pisał, bo jeszcze nie próbowałem).

Texas Instruments TI-92 Plus:

Z czystym sumieniem mogę polecić ten kalkulator każdeu fizykowi.

O innych modelach sie nie wypowiadam, bo używałem tylko dwóch wyżej wymienionych. Z drugiego z nich jestem tak zadowolony, że przez najbliższy czas nie będę nawet myślał o jego zmianie.

goto

Goto widzę już ostro zaczął. Mathematica, Latex… Więc dla rozładowania atmosfery ja napisze jeszcze trochę na pograniczu fizyki i ogólnego.

Piętnaście minut temu usiadłem sobie przed kompem celem zapoznania się z terminami kolokwiów. Patrzę na mechanikę klasyczną, termin ładny, długa przerwa, przyglądam się lepiej, szok… DLACZEGO KURNA NA SMYCZKOWEJ?? przecież to… przecież to… jak tam się w ogóle jechało? Tym sposobem naszła mnie refleksja na temat budynków naszego kochanego wydziału.

Główny budynek każdy zna – Hoża 69 – zaczyna się ślicznym szlabanem który trzeba ominąć, potem hmm… skwerek z ławkami i parking. Budynek sam w sobie – jakby nie patrzeć – całkiem ładny. Wchodzimy do środka – miła pani w szatni, panie w dziekanacie (tam już tylko niektóre są miłe) w zasadzie to jak wszedłem pierwszy raz ogarnął mnie respekt przed tym budynkiem… Zwłaszcza widząc to zagęszczenie fizyków. Kilku na metr kwadratowy. Większość jest upchniętych w budynku IPJ, także nie jesteśmy zbytnio narażeni na spotkanie. Czasami może to i dobrze… O Hożej można by pisać i pisać, ale po co skoro ten budynek jest nudny? przejdźmy do następnych… ciekawszych…

Zaraz obok mieści się budynek KMMF. Ten już jest ciekawszym budynkiem. Na dzień dobry wita nas zamknięta brama i zamek szyfrowy, do którego kod jest ściśle tajny, i niesamowicie trudny. Oczywistym jest że nie napiszę go tutaj, ponieważ Dr. Grabowska przestrzegła nas przed podawania numeru osobom postronnym. Po przejściu bramy, znajdujemy się na czymś co kiedyś w dawnych warowniach nazywano dziedzińcem. Czyli placyk otoczony z czterech stron murami. Ciekawa jest na przykład historia założenia wspomnianego wcześniej zamka szyfrowego. Otóż, w zamierzchłych czasach, kiedy dzisiejsi studenci palili papierosy po szatniach, zamka tego nie było. Wchodził kto chciał i kiedy chciał (można to porównać z jednym z warszawskich akademików). A że budynek wyglądał tak jak wygląda teraz, czyli jakby nie porównywać jak podziemia dworca centralnego – upatrzyło sobie to miejsce wszelkie menelstwo z okolicy by tam spożywać oranżadę. Osobie odpowiedzialnej za budynek KMMF, nie spodobało się to, tak więc założono zamek. Dlaczego wybrano tak trudne hasło – nikt nie wie.

Dochodzimy do drzwi wejściowych… Przyglądamy się i zastanawiamy jakim cudem te drzwi w ogóle się trzymają. Takie ułożenie drzwi z fizycznego punktu widzenia to na pewno nie jest poziom równowagi trwałej… A to do cholery jest budynek fizyki! Nie zrażając się tym, wpisujemy identyczny z poprzednim kod na drugim zamku cyfrowym i wchodzimy. Ogarnia nas ciemność, tak wielka jak że aż niewyobrażalna, która po chwili przeobraża się w ciemny, ciasny, zaniedbany acz posprzątany korytarz – klatkę schodową. Chwila zastanowienia – które to piętro? 5.. – wchodzimy na parter (nawet na parter mamy schody) i widzimy windę… uff – mija nas w takim razie wchodzenie na 5 piętro po tych niesamowicie niewygodnych kręconych schodach.

Podchodzimy do drzwi (wrota piekieł – tak bym to nazwał) naciskamy guzik wołacza windy… 99% nieprzyzwyczajonych studentów, odskakuje w tym momencie od drzwi (huk ruszającej windy jest niesamowity) i zaczynają się wątpliwości czy jedziemy tą windą czy nie, bo dopiero teraz oczy wystarczająco przyzwyczaiły się do ciemności by konstrukcję windy zobaczyć. Szyb, wije się pomiędzy schodami, oddzielony od nich jedynie siatką. Winda jadąc wyje, trzask i strzela. Jeżeli jesteśmy na tyle odważni (wielu już dawno jest piechotką na 5 piętrze) wchodzimy. Zamykamy jedne drzwi, zamykamy drzwi od wewnątrz, naciskamy 5 i nic… naciskamy mocniej – BUCH! winda ruszyła zgniatając lekko kręgosłup. Można by się zastanowić czy to wynik przeciążeń, czy może wynik skrócenia relatywistycznego wynikłego z ogromnej prędkości. Winda ruszyła. i nie daj Boże otworzyć teraz drzwi (co prawda dla nie których zatrzymanie się windy między piętrami jest zabawą, jednak widna nie zawsze chce ruszyć z powrotem). Po dojechaniu na 5 piętro winda staje gwałtownie co znowu powoduje wydłużeniu się naszego ciała w kierunku normalnym do podłogi. Sukces.

Po wyjściu z windy widzimy tablicę ogłoszeń, odrapane ściany oraz drzwi po lewej, które z reguły przekraczamy idąc na egzamin tudzież konsultacje, które po przeżyciach z windą (która nie jest jeszcze najciekawszą windą w budynkach UW – ale o tym później) są czymś całkiem przyjemnym.

Pozostało jeszcze kilka ciekawych budynków, między innymi wspomniana Smyczkowa, jednak na nie pożalę się kiedy indziej. Inaczej Wpis ten stanie się tak długi, iż nikt nawet go nie zacznie czytać.

Much